题目内容
设抛物线C的方程为x2=4y,M为直线l:y=-m(m>0)上任意一点,过点M作抛物线C的两条切线MA,MB,切点分别为A,B.
(Ⅰ)当M的坐标为(0,-l)时,求过M,A,B三点的圆的标准方程,并判断直线l与此圆的位置关系;
(Ⅱ)当m变化时,试探究直线l上是否存在点M,使MA⊥MB?若存在,有几个这样的点,若不存在,请说明理由.
(Ⅰ)当M的坐标为(0,-l)时,求过M,A,B三点的圆的标准方程,并判断直线l与此圆的位置关系;
(Ⅱ)当m变化时,试探究直线l上是否存在点M,使MA⊥MB?若存在,有几个这样的点,若不存在,请说明理由.
分析:(Ⅰ)设过M点的切线方程,代入x2=4y,整理得x2-4kx+4=0,令△=0,可得A,B的坐标,利用M到AB的中点(0,1)的距离为2,可得过M,A,B三点的圆的方程,从而可判断圆与直线l:y=-1相切;
(Ⅱ)设切点分别为A(x1,y1)、B(x2,y2),直线l上的点为M(x0,y0),可得x1,x2是方程x2-2x0x+4y0=0的两实根,从而kMA•kMB=
•
=y0,由此可得结论.
(Ⅱ)设切点分别为A(x1,y1)、B(x2,y2),直线l上的点为M(x0,y0),可得x1,x2是方程x2-2x0x+4y0=0的两实根,从而kMA•kMB=
| x1 |
| 2 |
| x2 |
| 2 |
解答:解:(Ⅰ)当M的坐标为(0,-1)时,设过M点的切线方程为y=kx-1,代入x2=4y,整理得x2-4kx+4=0,①
令△=(4k)2-4×4=0,解得k=±1,
代入方程①得x=±2,故得A(2,1),B(-2,1).
因为M到AB的中点(0,1)的距离为2,从而过M,A,B三点的圆的标准方程为x2+(y-1)2=4.
∵圆心坐标为(0,1),半径为2,
∴圆与直线l:y=-1相切.…(6分)
(Ⅱ)设切点分别为A(x1,y1)、B(x2,y2),直线l上的点为M(x0,y0),
过抛物线上点A(x1,y1)的切线方程为y-y1=k(x-x1),因为
=4y1,k=
,
从而过抛物线上点A(x1,y1)的切线方程为y-y1=
(x-x1),
又切线过点M(x0,y0),所以得y0=
x0-
,即
-2x0x1+4y0=0.
同理可得过点B(x2,y2)的切线方程为
-2x0x2+4y0=0,…(8分)
因为kMA=
,kMB=
,且x1,x2是方程x2-2x0x+4y0=0的两实根,
所以
所以kMA•kMB=
•
=y0,
当y0=-1,即m=1时,直线l上任意一点M均有MA⊥MB,…(10分)
当y0≠-1,即m≠1时,MA与MB不垂直.
综上所述,当m=1时,直线l上存在无穷多个点M,使MA⊥MB,当m≠1时,直线l上不存在满足条件的点M.…(12分)
令△=(4k)2-4×4=0,解得k=±1,
代入方程①得x=±2,故得A(2,1),B(-2,1).
因为M到AB的中点(0,1)的距离为2,从而过M,A,B三点的圆的标准方程为x2+(y-1)2=4.
∵圆心坐标为(0,1),半径为2,
∴圆与直线l:y=-1相切.…(6分)
(Ⅱ)设切点分别为A(x1,y1)、B(x2,y2),直线l上的点为M(x0,y0),
过抛物线上点A(x1,y1)的切线方程为y-y1=k(x-x1),因为
| x | 2 1 |
| x1 |
| 2 |
从而过抛物线上点A(x1,y1)的切线方程为y-y1=
| x1 |
| 2 |
又切线过点M(x0,y0),所以得y0=
| x1 |
| 2 |
| x12 |
| 4 |
| x | 2 1 |
同理可得过点B(x2,y2)的切线方程为
| x | 2 2 |
因为kMA=
| x1 |
| 2 |
| x2 |
| 2 |
所以
|
所以kMA•kMB=
| x1 |
| 2 |
| x2 |
| 2 |
当y0=-1,即m=1时,直线l上任意一点M均有MA⊥MB,…(10分)
当y0≠-1,即m≠1时,MA与MB不垂直.
综上所述,当m=1时,直线l上存在无穷多个点M,使MA⊥MB,当m≠1时,直线l上不存在满足条件的点M.…(12分)
点评:本题考查圆的方程,考查抛物线的切线,考查分类讨论的数学思想,确定切线方程是关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 如图,设抛物线C的方程为y2=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=
如图,设抛物线C的方程为y2=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN= =4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=
=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN= B.-
B.-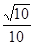 D.-
D.-