题目内容
 如图,设抛物线C的方程为y2=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=
如图,设抛物线C的方程为y2=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=-
| ||
| 10 |
-
.
| ||
| 10 |
分析:由物线C的方程为y2=4x,知P(-1,0),F(1,0),由焦点F且垂直于x轴的直线交抛物线于M、N两点,知M(1,2),N(1,-2),所以直线PM的方程为y=x+1,直线ON的方程为y=-2x,解方程组
,得Q(-
,
).所以
=(
,
),
=(
,-
),由此能求出cos∠MQN.
|
| 1 |
| 3 |
| 2 |
| 3 |
| QM |
| 4 |
| 3 |
| 4 |
| 3 |
| QN |
| 4 |
| 3 |
| 8 |
| 3 |
解答:解:如图,∵物线C的方程为y2=4x,O为坐标原点,
P为抛物线的准线与其对称轴的交点,
∴P(-1,0),
F(1,0),
∵焦点F且垂直于x轴的直线交抛物线于M、N两点,
∴M(1,2),N(1,-2),
∵直线PM过P(-1,0),M(1,2),
∴直线PM的方程为
=1,即y=x+1,
∵直线NO过点O(0,0),N(1,-2),
∴直线ON的方程是
=
,即y=-2x,
∴解方程组
,得Q(-
,
).
∴
=(
,
),
=(
,-
),
∴cos∠MQN=cos<
,
>=
=-
.
故答案为:-
.

P为抛物线的准线与其对称轴的交点,
∴P(-1,0),
F(1,0),
∵焦点F且垂直于x轴的直线交抛物线于M、N两点,
∴M(1,2),N(1,-2),
∵直线PM过P(-1,0),M(1,2),
∴直线PM的方程为
| y |
| x+1 |
∵直线NO过点O(0,0),N(1,-2),
∴直线ON的方程是
| y |
| x |
| -2 |
| 1 |
∴解方程组
|
| 1 |
| 3 |
| 2 |
| 3 |
∴
| QM |
| 4 |
| 3 |
| 4 |
| 3 |
| QN |
| 4 |
| 3 |
| 8 |
| 3 |
∴cos∠MQN=cos<
| QM |
| QN |
| ||||||||
|
| ||
| 10 |
故答案为:-
| ||
| 10 |
点评:本题主要考查直线与圆锥曲线的综合应用能力,综合性强,难度大,是高考的重点,易错点是抛物线知识体系不牢固.本题具体涉及到轨迹方程的求法及直线与抛物线的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
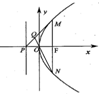 如图,设抛物线C的方程为y2=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=________.
如图,设抛物线C的方程为y2=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=________.