题目内容
设抛物线C的方程为x2=4y,M(x,y)为直线l:y=-m(m>0)上任意一点,过点M作抛物线C的两条切线MA,MB,切点分别为A,B.(1)当M的坐标为(0,-1)时,求过M,A,B三点的圆的方程,并判断直线l与此圆的位置关系;
(2)求证:直线AB恒过定点(0,m).
【答案】分析:(1)设过M点的切线方程,代入x2=4y,整理得x2-4kx+4=0,令△=0,可得A,B的坐标,利用M到AB的中点(0,1)的距离为2,可得过M,A,B三点的圆的方程,从而可判断圆与直线l:y=-1相切;
(2)证法一:设切点分别为A(x1,y1),B(x2,y2),过抛物线上点A(x1,y1)的切线方程为 ,代入x2=4y,消元,利用△=0,即可确定
,代入x2=4y,消元,利用△=0,即可确定 ,利用切线过点M(x,y),所以可得
,利用切线过点M(x,y),所以可得 ,同理可得
,同理可得 ,由此可得直线AB的方程,从而可得结论;
,由此可得直线AB的方程,从而可得结论;
证法二:设过M(x,y)的抛物线的切线方程为 (k≠0),代入x2=4y,消去y,利用韦达定理,确定直线AB的方程,从而可得结论;
(k≠0),代入x2=4y,消去y,利用韦达定理,确定直线AB的方程,从而可得结论;
证法三:利用导数法,确定切线的斜率,得切线方程,由此可得直线AB的方程,从而可得结论.
解答:(1)解:当M的坐标为(0,-1)时,设过M点的切线方程为y=kx-1,代入x2=4y,整理得x2-4kx+4=0,
令△=(4k)2-4×4=0,解得k=±1,
代入方程得x=±2,故得A(2,1),B(-2,1),…(2分)
因为M到AB的中点(0,1)的距离为2,
从而过M,A,B三点的圆的方程为x2+(y-1)2=4.
∵圆心坐标为(0,1),半径为2,∴圆与直线l:y=-1相切…(4分)
(2)证法一:设切点分别为A(x1,y1),B(x2,y2),过抛物线上点A(x1,y1)的切线方程为 ,代入x2=4y,整理得x2-4kx+4(kx1-y1)=0△=(4k)2-4×4(kx1-y1)=0,又因为
,代入x2=4y,整理得x2-4kx+4(kx1-y1)=0△=(4k)2-4×4(kx1-y1)=0,又因为 ,所以
,所以 …(6分)
…(6分)
从而过抛物线上点A(x1,y1)的切线方程为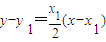 即
即
又切线过点M(x,y),所以得 ①即
①即 …(8分)
…(8分)
同理可得过点B(x2,y2)的切线为 ,
,
又切线过点M(x,y),所以得 ②…(10分)
②…(10分)
即 …(6分)
…(6分)
即点A(x1,y1),B(x2,y2)均满足 即xx=2(y+y),故直线AB的方程为xx=2(y+y)…(12分)
即xx=2(y+y),故直线AB的方程为xx=2(y+y)…(12分)
又M(x,y)为直线l:y=-m(m>0)上任意一点,故xx=2(y-m)对任意x成立,所以x=0,y=m,从而直线AB恒过定点(0,m)…(14分)
证法二:设过M(x,y)的抛物线的切线方程为 (k≠0),代入x2=4y,消去y,得x2-4kx-4(y-kx)=0△=(4k)2+4×4(y-kx)=0即:k2+xk+y=0…(6分)
(k≠0),代入x2=4y,消去y,得x2-4kx-4(y-kx)=0△=(4k)2+4×4(y-kx)=0即:k2+xk+y=0…(6分)
从而 ,
, 此时
此时 ,
,
所以切点A,B的坐标分别为 ,
, …(8分)
…(8分)
因为 ,
, ,
, ,
,
所以AB的中点坐标为 …(11分)
…(11分)
故直线AB的方程为 ,即xx=2(y+y)…(12分)
,即xx=2(y+y)…(12分)
又M(x,y)为直线l:y=-m(m>0)上任意一点,故xx=2(y-m)对任意x成立,所以x=0,y=m,从而直线AB恒过定点(0,m)…(14分)
证法三:由已知得 ,求导得
,求导得 ,切点分别为A(x1,y1),B(x2,y2),故过点A(x1,y1)的切线斜率为
,切点分别为A(x1,y1),B(x2,y2),故过点A(x1,y1)的切线斜率为 ,从而切线方程为
,从而切线方程为 即
即
…(7分)
又切线过点M(x,y),所以得 ①即
①即 …(8分)
…(8分)
同理可得过点B(x2,y2)的切线为 ,
,
又切线过点M(x,y),所以得 ②即
②即 …(10分)
…(10分)
即点A(x1,y1),B(x2,y2)均满足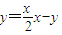 即xx=2(y+y),故直线AB的方程为xx=2(y+y)…(12分)
即xx=2(y+y),故直线AB的方程为xx=2(y+y)…(12分)
又M(x,y)为直线l:y=-m(m>0)上任意一点,故xx=2(y-m)对任意x成立,所以x=0,y=m,从而直线AB恒过定点(0,m)…(14分)
点评:本题考查圆的方程,考查抛物线的切线,考查直线恒过定点,确定切线方程,及直线AB的方程是关键.
(2)证法一:设切点分别为A(x1,y1),B(x2,y2),过抛物线上点A(x1,y1)的切线方程为
 ,代入x2=4y,消元,利用△=0,即可确定
,代入x2=4y,消元,利用△=0,即可确定 ,利用切线过点M(x,y),所以可得
,利用切线过点M(x,y),所以可得 ,同理可得
,同理可得 ,由此可得直线AB的方程,从而可得结论;
,由此可得直线AB的方程,从而可得结论;证法二:设过M(x,y)的抛物线的切线方程为
 (k≠0),代入x2=4y,消去y,利用韦达定理,确定直线AB的方程,从而可得结论;
(k≠0),代入x2=4y,消去y,利用韦达定理,确定直线AB的方程,从而可得结论;证法三:利用导数法,确定切线的斜率,得切线方程,由此可得直线AB的方程,从而可得结论.
解答:(1)解:当M的坐标为(0,-1)时,设过M点的切线方程为y=kx-1,代入x2=4y,整理得x2-4kx+4=0,
令△=(4k)2-4×4=0,解得k=±1,
代入方程得x=±2,故得A(2,1),B(-2,1),…(2分)
因为M到AB的中点(0,1)的距离为2,
从而过M,A,B三点的圆的方程为x2+(y-1)2=4.
∵圆心坐标为(0,1),半径为2,∴圆与直线l:y=-1相切…(4分)
(2)证法一:设切点分别为A(x1,y1),B(x2,y2),过抛物线上点A(x1,y1)的切线方程为
 ,代入x2=4y,整理得x2-4kx+4(kx1-y1)=0△=(4k)2-4×4(kx1-y1)=0,又因为
,代入x2=4y,整理得x2-4kx+4(kx1-y1)=0△=(4k)2-4×4(kx1-y1)=0,又因为 ,所以
,所以 …(6分)
…(6分)从而过抛物线上点A(x1,y1)的切线方程为
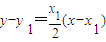 即
即
又切线过点M(x,y),所以得
 ①即
①即 …(8分)
…(8分)同理可得过点B(x2,y2)的切线为
 ,
,又切线过点M(x,y),所以得
 ②…(10分)
②…(10分)即
 …(6分)
…(6分)即点A(x1,y1),B(x2,y2)均满足
 即xx=2(y+y),故直线AB的方程为xx=2(y+y)…(12分)
即xx=2(y+y),故直线AB的方程为xx=2(y+y)…(12分)又M(x,y)为直线l:y=-m(m>0)上任意一点,故xx=2(y-m)对任意x成立,所以x=0,y=m,从而直线AB恒过定点(0,m)…(14分)
证法二:设过M(x,y)的抛物线的切线方程为
 (k≠0),代入x2=4y,消去y,得x2-4kx-4(y-kx)=0△=(4k)2+4×4(y-kx)=0即:k2+xk+y=0…(6分)
(k≠0),代入x2=4y,消去y,得x2-4kx-4(y-kx)=0△=(4k)2+4×4(y-kx)=0即:k2+xk+y=0…(6分)从而
 ,
, 此时
此时 ,
,
所以切点A,B的坐标分别为
 ,
, …(8分)
…(8分)因为
 ,
, ,
, ,
,所以AB的中点坐标为
 …(11分)
…(11分)故直线AB的方程为
 ,即xx=2(y+y)…(12分)
,即xx=2(y+y)…(12分)又M(x,y)为直线l:y=-m(m>0)上任意一点,故xx=2(y-m)对任意x成立,所以x=0,y=m,从而直线AB恒过定点(0,m)…(14分)
证法三:由已知得
 ,求导得
,求导得 ,切点分别为A(x1,y1),B(x2,y2),故过点A(x1,y1)的切线斜率为
,切点分别为A(x1,y1),B(x2,y2),故过点A(x1,y1)的切线斜率为 ,从而切线方程为
,从而切线方程为 即
即
…(7分)
又切线过点M(x,y),所以得
 ①即
①即 …(8分)
…(8分)同理可得过点B(x2,y2)的切线为
 ,
,又切线过点M(x,y),所以得
 ②即
②即 …(10分)
…(10分)即点A(x1,y1),B(x2,y2)均满足
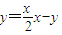 即xx=2(y+y),故直线AB的方程为xx=2(y+y)…(12分)
即xx=2(y+y),故直线AB的方程为xx=2(y+y)…(12分)又M(x,y)为直线l:y=-m(m>0)上任意一点,故xx=2(y-m)对任意x成立,所以x=0,y=m,从而直线AB恒过定点(0,m)…(14分)
点评:本题考查圆的方程,考查抛物线的切线,考查直线恒过定点,确定切线方程,及直线AB的方程是关键.

练习册系列答案
相关题目
 如图,设抛物线C的方程为y2=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=
如图,设抛物线C的方程为y2=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN= =4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=
=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN= B.-
B.-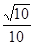 D.-
D.-