题目内容
已知抛物线方程为y2=2px(p>0).(1)若点
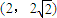 在抛物线上,求抛物线的焦点F的坐标和准线l的方程;
在抛物线上,求抛物线的焦点F的坐标和准线l的方程;(2)在(1)的条件下,若过焦点F且倾斜角为60°的直线m交抛物线于A、B两点,点M在抛物线的准线l上,直线MA、MF、MB的斜率分别记为kMA、kMF、kMB,求证:kMA、kMF、kMB成等差数列;
(3)对(2)中的结论加以推广,使得(2)中的结论成为推广后命题的特例,请写出推广命题,并给予证明.
说明:第(3)题将根据结论的一般性程度给予不同的评分.
【答案】分析:(1)由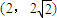 在抛物线上,得p=2,由此能导出抛物线的焦点F的坐标和准线l的方程.
在抛物线上,得p=2,由此能导出抛物线的焦点F的坐标和准线l的方程.
(2)抛物线的方程为y2=4x,过焦点F(1,0)且倾斜角为60°的直线m的方程为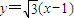 ,由
,由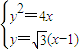 可得3x2-10x+3=0,解得点A、B的坐标为
可得3x2-10x+3=0,解得点A、B的坐标为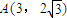 ,
,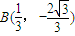 ,由此能导出kMA、kMF、kMB成等差数列.
,由此能导出kMA、kMF、kMB成等差数列.
(3)①推广命题:若抛物线的方程为y2=4x,过焦点F的直线m交抛物线于A、B两点,M为抛物线准线上的一点,直线MA、MF、MB的斜率分别记为kMA、kMF、kMB,则kMA、kMF、kMB成等差数列.再由抛物线的性质和韦达定理进行证明.
②推广命题:若抛物线的方程为y2=2px(p>0),过焦点F的直线m交抛物线于A、B两点,M为抛物线准线上的一点,直线MA、MF、MB的斜率分别记为kMA、kMF、kMB,则kMA、kMF、kMB成等差数列.再由抛物线的性质结合分类讨论思想进行证明.
解答:解:(1)∵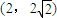 在抛物线上,由
在抛物线上,由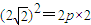 得p=2
得p=2
∴抛物线的焦点坐标为F(1,0),
准线l的方程为x=-1
(2)证明:∵抛物线的方程为y2=4x,过焦点F(1,0)且倾斜角为60°的直线m的方程为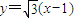
由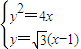 可得3x2-10x+3=0
可得3x2-10x+3=0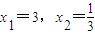
解得点A、B的坐标为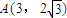 ,
,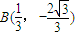
∵抛物线的准线方程为x=-1,设点M的坐标为M(-1,t),
则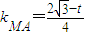 ,
,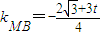 ,
,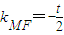 ,
,
由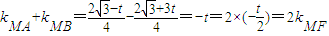
知kMA、kMF、kMB成等差数列.
(3)本小题可根考生不同的答题情况给予评分
①推广命题:若抛物线的方程为y2=4x,过焦点F的直线m交抛物线于A、B两点,M为抛物线准线上的一点,直线MA、MF、MB的斜率分别记为kMA、kMF、kMB,则kMA、kMF、kMB成等差数列.
证明:
抛物线y2=4x的焦点坐标为F(1,0),当直线l1平行于y轴时,
由(2)知命题成立.
设M点坐标为M(-1,t)
当直线m不平行于y轴时,设m的方程为y=k(x-1),其与抛物线的交点坐标为A(x1,y1)、B(x2,y2),则有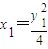 ,
,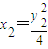
由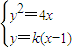 得ky2-4y-4k=0,即y1y2=-4
得ky2-4y-4k=0,即y1y2=-4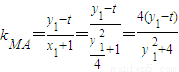 ,
,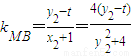
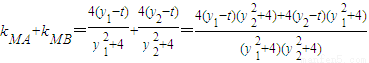 =
=
 ,∴kMA+kMB=2kMF,即kMA、kMF、kMB成等差数列
,∴kMA+kMB=2kMF,即kMA、kMF、kMB成等差数列
②推广命题:若抛物线的方程为y2=2px(p>0),过焦点F的直线m交抛物线于A、B两点,M为抛物线准线上的一点,直线MA、MF、MB的斜率分别记为kMA、kMF、kMB,则kMA、kMF、kMB成等差数列.
证明:抛物线的焦点F的坐标为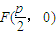 ,准线方程为
,准线方程为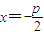 ,设M点坐标为
,设M点坐标为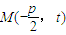
设m与抛物线的交点坐标为A(x1,y1)、B(x2,y2),则有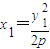 ,
,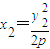
(ⅰ)当直线m平行于y轴时,直线m的方程为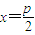 ,
,
此时有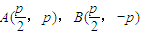 ,∴y1y2=-p2
,∴y1y2=-p2
(ⅱ)当直线m不平行于y轴时,直线m的方程可设为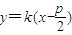
由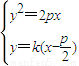 得
得 ∴y1y2=-p2
∴y1y2=-p2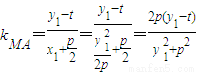 ,
,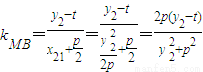
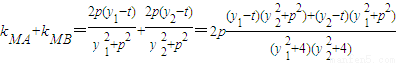 =
=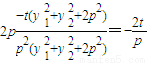
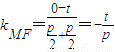 ,
,
∴kMA+kMB=2kMF,即kMA、kMF、kMB成等差数列
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与抛物线的相关知识,解题时要注意合理地进行等价转化.
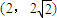 在抛物线上,得p=2,由此能导出抛物线的焦点F的坐标和准线l的方程.
在抛物线上,得p=2,由此能导出抛物线的焦点F的坐标和准线l的方程.(2)抛物线的方程为y2=4x,过焦点F(1,0)且倾斜角为60°的直线m的方程为
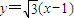 ,由
,由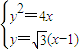 可得3x2-10x+3=0,解得点A、B的坐标为
可得3x2-10x+3=0,解得点A、B的坐标为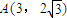 ,
,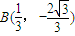 ,由此能导出kMA、kMF、kMB成等差数列.
,由此能导出kMA、kMF、kMB成等差数列.(3)①推广命题:若抛物线的方程为y2=4x,过焦点F的直线m交抛物线于A、B两点,M为抛物线准线上的一点,直线MA、MF、MB的斜率分别记为kMA、kMF、kMB,则kMA、kMF、kMB成等差数列.再由抛物线的性质和韦达定理进行证明.
②推广命题:若抛物线的方程为y2=2px(p>0),过焦点F的直线m交抛物线于A、B两点,M为抛物线准线上的一点,直线MA、MF、MB的斜率分别记为kMA、kMF、kMB,则kMA、kMF、kMB成等差数列.再由抛物线的性质结合分类讨论思想进行证明.
解答:解:(1)∵
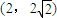 在抛物线上,由
在抛物线上,由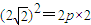 得p=2
得p=2∴抛物线的焦点坐标为F(1,0),
准线l的方程为x=-1
(2)证明:∵抛物线的方程为y2=4x,过焦点F(1,0)且倾斜角为60°的直线m的方程为
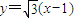
由
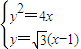 可得3x2-10x+3=0
可得3x2-10x+3=0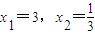
解得点A、B的坐标为
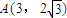 ,
,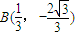
∵抛物线的准线方程为x=-1,设点M的坐标为M(-1,t),
则
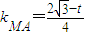 ,
,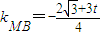 ,
,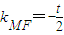 ,
,由
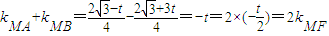
知kMA、kMF、kMB成等差数列.
(3)本小题可根考生不同的答题情况给予评分
①推广命题:若抛物线的方程为y2=4x,过焦点F的直线m交抛物线于A、B两点,M为抛物线准线上的一点,直线MA、MF、MB的斜率分别记为kMA、kMF、kMB,则kMA、kMF、kMB成等差数列.
证明:
抛物线y2=4x的焦点坐标为F(1,0),当直线l1平行于y轴时,
由(2)知命题成立.
设M点坐标为M(-1,t)
当直线m不平行于y轴时,设m的方程为y=k(x-1),其与抛物线的交点坐标为A(x1,y1)、B(x2,y2),则有
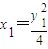 ,
,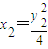
由
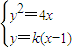 得ky2-4y-4k=0,即y1y2=-4
得ky2-4y-4k=0,即y1y2=-4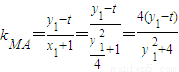 ,
,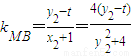
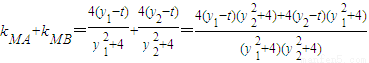 =
=
 ,∴kMA+kMB=2kMF,即kMA、kMF、kMB成等差数列
,∴kMA+kMB=2kMF,即kMA、kMF、kMB成等差数列②推广命题:若抛物线的方程为y2=2px(p>0),过焦点F的直线m交抛物线于A、B两点,M为抛物线准线上的一点,直线MA、MF、MB的斜率分别记为kMA、kMF、kMB,则kMA、kMF、kMB成等差数列.
证明:抛物线的焦点F的坐标为
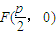 ,准线方程为
,准线方程为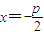 ,设M点坐标为
,设M点坐标为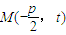
设m与抛物线的交点坐标为A(x1,y1)、B(x2,y2),则有
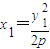 ,
,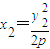
(ⅰ)当直线m平行于y轴时,直线m的方程为
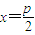 ,
,此时有
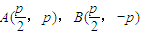 ,∴y1y2=-p2
,∴y1y2=-p2(ⅱ)当直线m不平行于y轴时,直线m的方程可设为
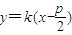
由
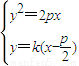 得
得 ∴y1y2=-p2
∴y1y2=-p2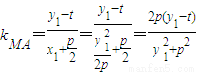 ,
,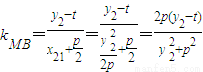
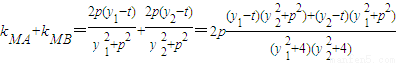 =
=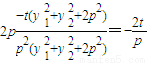
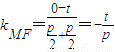 ,
,∴kMA+kMB=2kMF,即kMA、kMF、kMB成等差数列
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与抛物线的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 如图,已知抛物线方程为y2=8x.直线l1过抛物线的焦点F,且倾斜角为45°,直线l1与抛物线相交于C、D两点,O为原点.
如图,已知抛物线方程为y2=8x.直线l1过抛物线的焦点F,且倾斜角为45°,直线l1与抛物线相交于C、D两点,O为原点.