题目内容
 如图,已知抛物线方程为y2=8x.直线l1过抛物线的焦点F,且倾斜角为45°,直线l1与抛物线相交于C、D两点,O为原点.
如图,已知抛物线方程为y2=8x.直线l1过抛物线的焦点F,且倾斜角为45°,直线l1与抛物线相交于C、D两点,O为原点.(1)写出直线l1方程
(2)求CD的长度.
分析:(1)由题意可得,抛物线为y2=8x的焦点,然后由倾斜角求出直线的斜率,即可求解
(2)联立方程
,设C(x1,y1),D(x2,y2),根据方程的根与系数关系可求x1+x2,代入焦半径公式可求
(2)联立方程
|
解答:解:(1)由题意可得,抛物线为y2=8x的焦点为(2,0)
∴直线线l1方程为y=x-2即x-y-2=0
(2)联立方程
可得x2-12x+4=0
设C(x1,y1),D(x2,y2)
则x1+x2=12
由抛物线的焦半径公式可得CD=CF+FD=x1+
p+x2+
p=12+4=16
∴直线线l1方程为y=x-2即x-y-2=0
(2)联立方程
|
设C(x1,y1),D(x2,y2)
则x1+x2=12
由抛物线的焦半径公式可得CD=CF+FD=x1+
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了直线方程的求解,直线与抛物线的位置关系的应用,抛物线的焦半径公式的应用是求解(2)的关键

练习册系列答案
相关题目
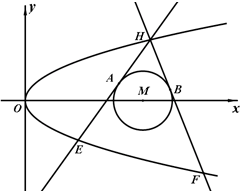 (2012•辽宁模拟)如图,已知抛物线C:y2=2px和⊙M:(x-4)2+y2=1,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线与⊙M相切于A、两点,分别交抛物线为E、F两点,圆心点M到抛物线准线的距离为
(2012•辽宁模拟)如图,已知抛物线C:y2=2px和⊙M:(x-4)2+y2=1,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线与⊙M相切于A、两点,分别交抛物线为E、F两点,圆心点M到抛物线准线的距离为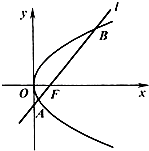 如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A、B两点.
如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A、B两点.
