Question

（2013•闵行区二模）已知函数f(x)=x|x-a|-

1

4

，x∈R．
（1）当a=1时，指出f（x）的单调递减区间和奇偶性（不需说明理由）；
（2）当a=1时，求函数y=f（2^x）的零点；
（3）若对任何x∈[0，1]不等式f（x）＜0恒成立，求实数a的取值范围．

Answer 1

分析：（1）当a=1时，利用分段函数的图象得出函数的单调递减区间和函数f（x）既不是奇函数也不是偶函数；
（2）当a=1时，f(x)=x|x-1|-

1

4

，欲求函数y=f（2^x）的零点，即求对应方程的根．由f（2^x）=0解得x的值即可；
（3）当x=0时，a取任意实数，不等式f（x）＜0恒成立，故只需考虑x∈（0，1]，此时原不等式变为|x-a|＜

1

4x

，即x-

1

4x

＜a＜x+

1

4x

．再构造函数，研究其最值即可得出实数a的取值范围．

解答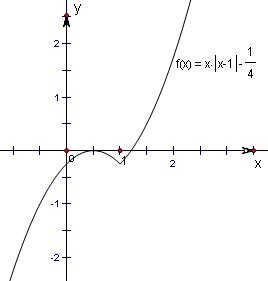：解：（1）当a=1时，函数的单调递减区间为[

1

2

，1]…（2分）
函数f（x）既不是奇函数也不是偶函数．        …（2分）
（2）当a=1时，f(x)=x|x-1|-

1

4

，
由f（2^x）=0得2x|2x-1|-

1

4

=0…（2分）
即

2x≥1 (2x)2-2x- 1 4 =0

或

2x＜1 (2x)2-2x+ 1 4 =0

…（2分）
解得2x=

1+ 2

2

或2x=

1- 2

2

(舍)，或2x=

1

2

所以x=log2

1+ 2

2

=log2(1+

2

)-1或x=-1．    …（2分）
（3）当x=0时，a取任意实数，不等式f（x）＜0恒成立，
故只需考虑x∈（0，1]，此时原不等式变为|x-a|＜

1

4x

即x-

1

4x

＜a＜x+

1

4x

…（2分）
故(x-

1

4x

)max＜a＜(x+

1

4x

)min，x∈(0，1]
又函数g(x)=x-

1

4x

在（0，1]上单调递增，∴(x-

1

4x

)max=g(1)=

3

4

…（2分）
函数h(x)=x+

1

4x

在(0，

1

2

]上单调递减，在[

1

2

，1]上单调递增，
∴(x+

1

4x

)min=h(

1

2

)=1；
所以

3

4

＜a＜1，即实数a的取值范围是(

3

4

，1)．…（2分）

点评：本题以分段函数为载体，考查函数的奇偶性单调性、恒成立等问题，解题的关键是等价转化，构造新函数．