Question

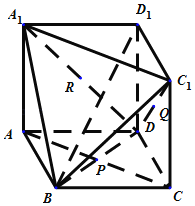
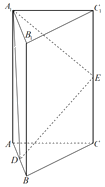
【题目】将正方体ABCD﹣A1B1C1D1沿三角形A1BC1所在平面削去一角可得到如图所示的几何体.

（1）连结BD,BD1,证明:平面BDD1⊥平面A1BC1;

（2）已知P,Q,R分别是正方形ABCDCDD1C1ADD1A1的中心(即对角线交点),证明:平面PQR∥平面A1BC1.

Answer 1

【答案】（1）答案见解析.（2）答案见解析

【解析】

（1）连接AC,证明A1C1⊥平面BDD1, 平面BDD1⊥平面A1BC1即得证;（2）连接A1D,BD,C1D,证明PQ∥平面A1BC1,PR∥平面A1BC1, 平面PQR∥平面A1BC1即得证.

（1）连接AC,∵正方体ABCD﹣A1B1C1D1,

∴AA1∥CC1,

∴A,A1,C,C1共面,

∵正方体ABCD﹣A1B1C1D1,

∴DD1⊥平面A1C1D1,

∵A1C1在平面A1C1D1内,

∴DD1⊥A1C1,

∵正方体ABCD﹣A1B1C1D1,

∴四边形ABCD为正方形,

∴AC⊥BD,

∵正方体ABCD﹣A1B1C1D1,

∴AA1⊥平面ABCD,

∵BD在平面A1C1D1内,

∴AA1⊥BD,

∵AC∩AA1=A且都在平面AA1C1C捏,

∴BD⊥平面AA1C1C,

∵A1C1在平面AA1C1C内,

∴BD⊥A1C1,

∵BD∩DD1=D,且都在平面BDD1内,

∴A1C1⊥平面BDD1,

∵A1C1在平面A1BC1内,

∴平面BDD1⊥平面A1BC1;

（2）连接A1D,BD,C1D,

∵P,Q,R分别是正方形ABCD,CDD1C1,ADD1A1的中心,

∴P,Q,R分别是BD,C1D,A1D的中点,

∴PQ∥BC1,

∵BC1在平面A1BC1内,PQ不在平面A1BC1内,

∴PQ∥平面A1BC1,

同理可得PR∥平面A1BC1,

又PQ∩PR=P且都在平面PQR内,

∴平面PQR∥平面A1BC1.