Question

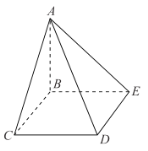
【题目】如图所示是一个上下底面均是边长为2的正三角形的直三棱柱,且该直三棱柱的高为4,D为AB的中点,E为CC1的中点.

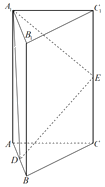
（1）求DE与平面ABC夹角的正弦值;

（2）求二面角A﹣A1D﹣E的余弦值.

Answer 1

【答案】（1）.（2）

【解析】

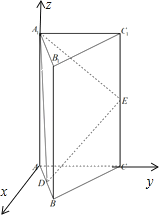
（1）如图所示,建立空间直角坐标系.利用向量法求DE与平面ABC夹角的正弦值;（2）利用向量法求二面角A﹣A1D﹣E的余弦值.

（1）如图所示,建立空间直角坐标系.

D(,,0),E(0,2,2),,,2),

平面ABC的法向量为(0,0,1).

∴DE与平面ABC夹角的正弦值=|cos,|.

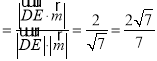（2）设平面A1DE的法向量为(x,y,z),由0,可得y+2z=0,2y﹣2z=0,

取(7,,).

同理可得平面AA1D的法向量,,0),

∴cos,.

∴二面角A﹣A1D﹣E的余弦值为.