题目内容
已知△ABC中,向量| m |
| 3 |
| n |
| m |
| n |
(1)求角A;
(2)若角A,B,C所对的边分别为a,b,c,且a=
| 3 |
分析:(1)利用向量的数量积,直接计算,根据A是三角形内角,求角A;
(2)用a=
和A,求出三角形外接圆直径,写出三角形面积表达式,然后利用积化和差公式,化简表达式,求△ABC的面积的最大值.
(2)用a=
| 3 |
解答:解:(1)
•
=1=-cosA+
sinA,
所以 sin(A-
)=
因为A 是三角形内角,所以A=
(2)三角形ABC的外接圆的半径为R,所以 2R=
=2,
S=
bcsinA=
2R×2R×sinAsinBsinC
=
[cos(B-C)-cos(B+C)]
=
cos(B-C)+
当B=C时,S取得最大值,最大值是:
| m |
| n |
| 3 |
所以 sin(A-
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
(2)三角形ABC的外接圆的半径为R,所以 2R=
| ||
sin
|
S=
| 1 |
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
=
| ||
| 2 |
| ||
| 4 |
当B=C时,S取得最大值,最大值是:
3
| ||
| 4 |
点评:本题考查平面向量数量积的运算,积化和差公式,正弦定理,考查学生分析问题解决问题的能力,是中档题.

练习册系列答案
相关题目
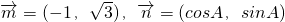 ;且
;且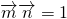 .
. ,求△ABC的面积的最大值.
,求△ABC的面积的最大值.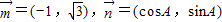 ;且
;且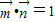 .
.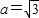 ,求△ABC的面积的最大值.
,求△ABC的面积的最大值.