题目内容
已知△ABC中,向量
=(-1,
),
=(cosA,sinA);且
•
=1.
(1)求角A;
(2)若角A,B,C所对的边分别为a,b,c,且a=
,求△ABC的面积的最大值.
| m |
| 3 |
| n |
| m |
| n |
(1)求角A;
(2)若角A,B,C所对的边分别为a,b,c,且a=
| 3 |
(1)
•
=1=-cosA+
sinA,
所以 sin(A-
)=
因为A 是三角形内角,所以A=
(2)三角形ABC的外接圆的半径为R,所以 2R=
=2,
S=
bcsinA=
2R×2R×sinAsinBsinC
=
[cos(B-C)-cos(B+C)]
=
cos(B-C)+
当B=C时,S取得最大值,最大值是:
| m |
| n |
| 3 |
所以 sin(A-
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
(2)三角形ABC的外接圆的半径为R,所以 2R=
| ||
sin
|
S=
| 1 |
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
=
| ||
| 2 |
| ||
| 4 |
当B=C时,S取得最大值,最大值是:
3
| ||
| 4 |

练习册系列答案
相关题目
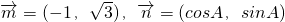 ;且
;且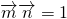 .
. ,求△ABC的面积的最大值.
,求△ABC的面积的最大值.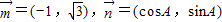 ;且
;且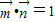 .
.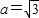 ,求△ABC的面积的最大值.
,求△ABC的面积的最大值.