题目内容
已知△ABC中，向量
=（x，2x），
=（3x，2），且∠BAC是锐角，则x的取值范围是
| AB |
| AC |
（-∞，-
）∪（0，
）∪（
，+∞）
| 4 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
（-∞，-
）∪（0，
）∪（
，+∞）
．| 4 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
分析：由题意可得
•
＞0，且
和
不共线，∴3x•x+2•2x＞0，且 x•2-2x•3x≠0．由此求得x的取值范围
| AB |
| AC |
| AB |
| AC |
解答：解：由题意可得
•
＞0，且
和
不共线，∴3x•x+2•2x＞0，且 x•2-2x•3x≠0．
解得 x＜-
，或 0＜x＜
，或 x＞
，
故答案为 （-∞，-
）∪（0，
）∪（
，+∞）．
| AB |
| AC |
| AB |
| AC |
解得 x＜-
| 4 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
故答案为 （-∞，-
| 4 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
点评：本题主要考查两个向量共线的性质，两个向量的数量积的运算，属于中档题．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
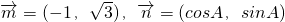；且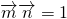
．
，求△ABC的面积的最大值．
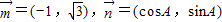；且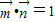
．
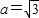，求△ABC的面积的最大值．