题目内容
已知△ABC中,向量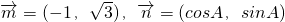 ;且
;且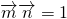 .
.
(1)求角A;
(2)若角A,B,C所对的边分别为a,b,c,且 ,求△ABC的面积的最大值.
,求△ABC的面积的最大值.
解:(1)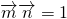 =
=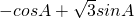 ,
,
所以 sin(A- )=
)= 因为A 是三角形内角,所以A=
因为A 是三角形内角,所以A=
(2)三角形ABC的外接圆的半径为R,所以 2R= =2,
=2,
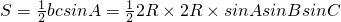
=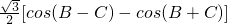
=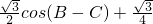
当B=C时,S取得最大值,最大值是:
分析:(1)利用向量的数量积,直接计算,根据A是三角形内角,求角A;
(2)用 和A,求出三角形外接圆直径,写出三角形面积表达式,然后利用积化和差公式,化简表达式,求△ABC的面积的最大值.
和A,求出三角形外接圆直径,写出三角形面积表达式,然后利用积化和差公式,化简表达式,求△ABC的面积的最大值.
点评:本题考查平面向量数量积的运算,积化和差公式,正弦定理,考查学生分析问题解决问题的能力,是中档题.
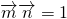 =
=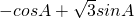 ,
,所以 sin(A-
 )=
)= 因为A 是三角形内角,所以A=
因为A 是三角形内角,所以A=
(2)三角形ABC的外接圆的半径为R,所以 2R=
 =2,
=2,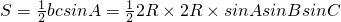
=
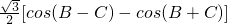
=
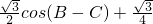
当B=C时,S取得最大值,最大值是:

分析:(1)利用向量的数量积,直接计算,根据A是三角形内角,求角A;
(2)用
 和A,求出三角形外接圆直径,写出三角形面积表达式,然后利用积化和差公式,化简表达式,求△ABC的面积的最大值.
和A,求出三角形外接圆直径,写出三角形面积表达式,然后利用积化和差公式,化简表达式,求△ABC的面积的最大值.点评:本题考查平面向量数量积的运算,积化和差公式,正弦定理,考查学生分析问题解决问题的能力,是中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
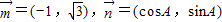 ;且
;且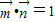 .
.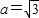 ,求△ABC的面积的最大值.
,求△ABC的面积的最大值.