题目内容
已知函数f(x)=4x2-mx+5在(-∞,-2]上是减函数,在[-2,+∞)上是增函数.
(1)求实数m的值;
(2)求函数f(x)当x∈[0,1]时的函数值的集合.
解:(1)、函数f(x)=4x2-mx+5的对称轴为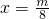 ,又因为函数f(x)=4x2-mx+5在(-∞,-2]上是减函数,在[-2,+∞)上是增函数.
,又因为函数f(x)=4x2-mx+5在(-∞,-2]上是减函数,在[-2,+∞)上是增函数.
所以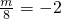 ,即m=-16.
,即m=-16.
(2)、由(1)得f(x)=4x2+16x+5,由f(x)在[-2,+∞)上是增函数,可得:f(x)在[0,1]上是增函数,
所以f(x)的最小值为f(0)=5,f(x)的最大值为f(1)=25,所以函数f(x)当x∈[0,1]时的函数值的集合为{x|5≤x≤25}.
分析:(1)、根据二次函数f(x)的单调区间确定出对称轴为x=-2,建方程解之.
(2)、根据已知f(x)的单调增区间判所求的区间上为增函数,求出最值后确定解集.
点评:考查二次函数的单调性和二次函数闭区间上的最值问题,注意第(2)问求的是函数值的集合,一定写为集合.
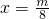 ,又因为函数f(x)=4x2-mx+5在(-∞,-2]上是减函数,在[-2,+∞)上是增函数.
,又因为函数f(x)=4x2-mx+5在(-∞,-2]上是减函数,在[-2,+∞)上是增函数.所以
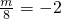 ,即m=-16.
,即m=-16.(2)、由(1)得f(x)=4x2+16x+5,由f(x)在[-2,+∞)上是增函数,可得:f(x)在[0,1]上是增函数,
所以f(x)的最小值为f(0)=5,f(x)的最大值为f(1)=25,所以函数f(x)当x∈[0,1]时的函数值的集合为{x|5≤x≤25}.
分析:(1)、根据二次函数f(x)的单调区间确定出对称轴为x=-2,建方程解之.
(2)、根据已知f(x)的单调增区间判所求的区间上为增函数,求出最值后确定解集.
点评:考查二次函数的单调性和二次函数闭区间上的最值问题,注意第(2)问求的是函数值的集合,一定写为集合.

练习册系列答案
相关题目