题目内容
5.若对任意α∈R,直线l:xcosα+ysinα=2sin(α+$\frac{π}{6}$)+4与圆C:(x-m)2+(y-$\sqrt{3}$m)2=1均无公共点,则实数m的取值范围是-$\frac{1}{2}$<m<$\frac{5}{2}$.
分析 求出圆心到直线的距离大于半径,结合对任意α∈R恒成立,即可求得实数m的取值范围.
解答 解:由题意,圆心到直线的距离d=|mcosα+$\sqrt{3}$msinα-2sin(α+$\frac{π}{6}$)-4|>1,
所以|(2m-2)sin(α+$\frac{π}{6}$)-4|>1,
所以(2m-2)sin(α+$\frac{π}{6}$)-4>1或(2m-2)sin(α+$\frac{π}{6}$)-4<-1,
所以-$\frac{1}{2}$<m<$\frac{5}{2}$.
故答案为:-$\frac{1}{2}$<m<$\frac{5}{2}$.
点评 本题考查直线与圆的位置关系,考查实数m的取值范围,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
16.已知数列{an}满足a1=1,|an-an-1|=$\frac{1}{{3}^{n}}$(n∈N,n≥2),且{a2n-1}是递减数列,{a2n}是递增数列,则12a10=( )
| A. | 6-$\frac{1}{{3}^{10}}$ | B. | 6-$\frac{1}{{3}^{9}}$ | C. | 11-$\frac{1}{{3}^{10}}$ | D. | 11-$\frac{1}{{3}^{9}}$ |
13.正实数数列{an}满足:a1=1,a9=7,且an+1=$\frac{({a}_{n}+1)^2-({a}_{n-1}+1)}{{a}_{n-1}+1}$(n∈N+,n≥2)则a5=( )
| A. | 4 | B. | 3 | C. | 16 | D. | 9 |
14.若$z=\frac{i}{1+2i}$,i为虚数单位,则|z|=( )
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
15.程序框图如图所示,若其输出结果是30,则判断框中填写的是( )
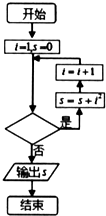

| A. | i<7? | B. | i<5? | C. | i>7? | D. | i>5? |
 如图是一个几何体的三视图,若它的体积是$3\sqrt{3}$,则a=$\sqrt{3}$,该几何体的表面积为2$\sqrt{3}$+18.
如图是一个几何体的三视图,若它的体积是$3\sqrt{3}$,则a=$\sqrt{3}$,该几何体的表面积为2$\sqrt{3}$+18.