题目内容
函数f(x)=( )|x|+1的值域为
)|x|+1的值域为
- A.(0,+∞)
- B.(0,
 )
) - C.(-∞,2]
- D.[
 ,2]
,2]
B
分析:求出指数的范围;由于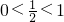 ,利用指数函数的单调性求出函数的值域.
,利用指数函数的单调性求出函数的值域.
解答:∵|x|+1≥1
∴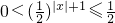
故选B
点评:本题考查利用指数函数的单调性求函数的值域.底数a>1时,指数函数单调递增;当0<a<1时,指数函数单调递减.
分析:求出指数的范围;由于
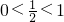 ,利用指数函数的单调性求出函数的值域.
,利用指数函数的单调性求出函数的值域.解答:∵|x|+1≥1
∴
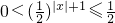
故选B
点评:本题考查利用指数函数的单调性求函数的值域.底数a>1时,指数函数单调递增;当0<a<1时,指数函数单调递减.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)满足f(0)=1,f(x+1)=
+f(x) (x∈R),则数列{f(n)}的前20项和为( )
| 3 |
| 2 |
| A、305 | B、315 |
| C、325 | D、335 |