题目内容
1．若实数x，y满足$\left\{\begin{array}{l}x≥y\\ y≥0\\ 2x+y-3≤0\end{array}\right.$则z=x+3y的最大值是（ ）| A． | 6 | B． | 4 | C． | $\frac{3}{2}$ | D． | 0 |
分析 先根据约束条件画出可行域，再利用几何意义求最值，z=x+3y表示直线在y轴上的截距，只需求出可行域直线在y轴上的截距最大值即可．
解答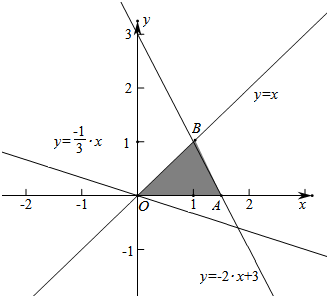 
解：先根据约束条件画出可行域，
当直线z=x+3y表示直线y=$-\frac{1}{3}$x+$\frac{z}{3}$，当过点B（1，1）时，
z最大是4；
故选：B
点评 本小题主要考查线性规划问题，以及利用几何意义求最值，属于基础题．
练习册系列答案
相关题目
12．关于复数z=$\frac{2}{-1+i}$的四个命题：
p1：复数z对应的点在第二象限，
p2：z2=2i，
p3：z的共轭复数为1+i，
p4：z的虚部为-1．
其中的真命题个数为（ ）
p1：复数z对应的点在第二象限，
p2：z2=2i，
p3：z的共轭复数为1+i，
p4：z的虚部为-1．
其中的真命题个数为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
9．过曲线C：y=$\frac{1}{x}$（x＞0）上一点P（x0，y0）作曲线C的切线，若切线的斜率为-4，则x0等于（ ）
| A． | 2 | B． | $\frac{1}{2}$ | C． | 4 | D． | $\frac{1}{4}$ |
6．在等比数列{an}（n∈N*）中，若a1=1，a4=$\frac{1}{8}$，则该数列的前10项和为（ ）
| A． | 2-$\frac{1}{2^4}$ | B． | 2-$\frac{1}{{2}^{9}}$ | C． | 2-$\frac{1}{{{2^{10}}}}$ | D． | 2-$\frac{1}{{{2^{11}}}}$ |
10．设$\overrightarrow{e_1}，\overrightarrow{e_2}$为两不共线的向量，则$\overrightarrow a=\overrightarrow{e_1}+λ\overrightarrow{e_2}$与$\overrightarrow b=-（{2\overrightarrow{e_2}-3\overrightarrow{e_1}}）$共线的条件是（ ）
| A． | λ=$\frac{3}{2}$ | B． | λ=$\frac{2}{3}$ | C． | λ=-$\frac{2}{3}$ | D． | λ=-$\frac{3}{2}$ |