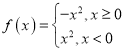题目内容
【题目】在平面直角坐标系![]() 中,已知半径为
中,已知半径为![]() 的圆
的圆![]() ,圆心在
,圆心在![]() 轴正半轴上,且与直线
轴正半轴上,且与直线![]() 相切.
相切.
(1)求圆![]() 的方程;
的方程;
(2)在圆![]() 上,是否存在点
上,是否存在点![]() ,满足
,满足![]() ,其中,点
,其中,点![]() 的坐标是
的坐标是![]() .若存在,指出有几个这样的点;若不存在,请说明理由;
.若存在,指出有几个这样的点;若不存在,请说明理由;
(3)若在圆![]() 上存在点
上存在点![]() ,使得直线
,使得直线![]() 与圆
与圆![]() 相交不同两点
相交不同两点![]() ,求
,求![]() 的取值范围.并求出使得
的取值范围.并求出使得![]() 的面积最大的点
的面积最大的点![]() 的坐标及对应的
的坐标及对应的![]() 的面积.
的面积.
【答案】(1)![]() ;(2)不存在点
;(2)不存在点![]() 满足条件;(3)
满足条件;(3)![]() ,
,![]() .
.
【解析】
试题分析:(1)设圆心坐标是![]() ,可根据点到直线距离公式求得
,可根据点到直线距离公式求得![]() ,即可得到圆
,即可得到圆![]() 的方程;(2)假设存在这样的点
的方程;(2)假设存在这样的点![]() ,则有
,则有![]() ,然后判断
,然后判断![]() 与
与![]() 有无交点即可;(3)根据圆心到直线的距离小于半径即可求
有无交点即可;(3)根据圆心到直线的距离小于半径即可求![]() 的取值范围,
的取值范围,![]() 的面积表示为关于
的面积表示为关于![]() 的函数,利用配方法可求最值.
的函数,利用配方法可求最值.
试题解析:(1)设圆心是![]() ,它到直线
,它到直线![]() 的距离是
的距离是![]() ,解得
,解得![]() 或
或![]() (舍去),所以,所求圆
(舍去),所以,所求圆![]() 的方程是
的方程是![]() .
.
(2)假设存在这样的点![]() ,则由
,则由![]() ,得
,得![]() .
.
即,点P在圆D:![]() 上,点P也在圆C:
上,点P也在圆C:![]() 上.
上.
因为![]() ,所以圆C与圆D外离,圆C与圆D没有公共点.所以,不存在点
,所以圆C与圆D外离,圆C与圆D没有公共点.所以,不存在点![]() 满足条件.
满足条件.
(3)存在,理由如下:因为点![]() 在圆
在圆![]() 上,所以
上,所以![]() ,
,![]() 且
且![]() .
.
因为原点到直线![]() 的距离
的距离![]() ,解得
,解得![]()
而![]() ,所以
,所以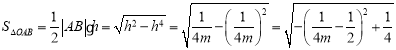 ,
,
因为![]() ,所以当
,所以当![]() ,即
,即![]() 时,
时,![]() 取得最大值
取得最大值![]() ,
,
此时点![]() 的坐标是
的坐标是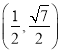 或
或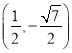 ,
,![]() 的面积的最大值是
的面积的最大值是![]() .
.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
【题目】为了选拔参加自行车比赛的选手,对自行车运动员甲、乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息;
(2)估计甲、乙两运动员的最大速度的平均数和方差,并判断谁参加比赛更合适.