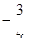题目内容
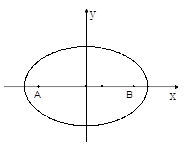
椭圆满足这样的光学性质:从椭圆的一个焦点发射的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.现有一个水平放置的椭圆形台球盘,满足方程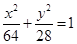 ,点
,点 是它的两个焦点.当静止的小球从点
是它的两个焦点.当静止的小球从点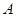 开始出发,沿直线运动,经椭圆壁反射后再回到点
开始出发,沿直线运动,经椭圆壁反射后再回到点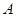 时,此时小球经过的路程可能是 ( )
时,此时小球经过的路程可能是 ( )
A.32或4或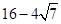 | B.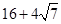 或28或 或28或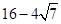 |
C.28或4或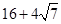 | D.32或28或4 |
D
解析

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
若双曲线过点 ,且渐近线方程为
,且渐近线方程为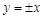 ,则双曲线的焦点( )
,则双曲线的焦点( )
A.在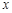 轴上 轴上 | B.在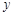 轴上 轴上 | C.在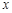 轴或 轴或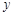 轴上 轴上 | D.无法判断是否在坐标轴上 |
已知双曲线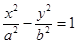 的一个焦点与抛物线y2=4x的焦点重合,且双曲线的离心率等于
的一个焦点与抛物线y2=4x的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为
,则该双曲线的方程为
A.5x2- y2=1? y2=1? | B.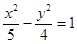 |
C. | D.5x2- y2=1 y2=1 |
双曲线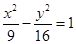 的焦点坐标是( )
的焦点坐标是( )
A.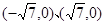 | B.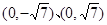 | C. | D.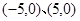 |
设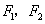 分别是双曲线
分别是双曲线 的左、右焦点,若双曲线上存在点
的左、右焦点,若双曲线上存在点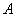 ,使
,使 且
且 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. | B. | C.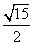 | D. |
给出下列曲线:
① 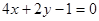 ;②
;② 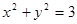 ;③
;③  ;④
;④ 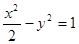 .
.
其中与直线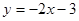 有公共点的所有曲线是 ( )
有公共点的所有曲线是 ( )
| A.①③ | B.②④ | C.①②③ | D.②③④ |
 ,虚轴的一个端点为
,虚轴的一个端点为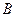 ,如果直线
,如果直线 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为
与该双曲线的一条渐近线垂直,那么此双曲线的离心率为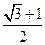
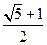
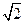

 、
、 分别是双曲线
分别是双曲线 的左、右焦点,
的左、右焦点, 是其右顶点,过
是其右顶点,过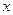 轴的垂线与双曲线的一个交点为
轴的垂线与双曲线的一个交点为 ,
, 是
是 ,则双曲线的离心率是
,则双曲线的离心率是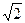
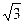
 的顶点,过点D(0,4)的直线
的顶点,过点D(0,4)的直线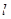 交抛物线
交抛物线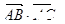 等于( )
等于( )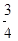 B.0 C.-3 D.
B.0 C.-3 D.