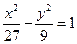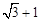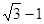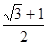题目内容
若双曲线过点 ,且渐近线方程为
,且渐近线方程为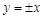 ,则双曲线的焦点( )
,则双曲线的焦点( )
A.在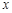 轴上 轴上 | B.在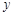 轴上 轴上 | C.在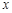 轴或 轴或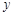 轴上 轴上 | D.无法判断是否在坐标轴上 |
A
解析考点:双曲线的简单性质.
分析:先假设焦点在x轴,根据渐近线方程设出双曲线方程,把点(m,n)代入方程,结果符合题意;再假设焦点在y轴时,把点(m,n)代入方程,根据m和n的大小可知,不符合题意.最后综合可得结论.
解:假设焦点在x轴上,根据渐近线方程为y=±x可知双曲线的实轴和虚轴长度相同,
设双曲线方程为x2-y2=t2(t≠0)
∵m>n,∴m2-n2=t2符合;
假设焦点在y轴,依题意可设双曲线方程为y2-x2=t2
把点(m,n)代入双曲线方程得n2-m2=t2
∵m>n
∴n2-m2<0,与n2-m2=t2>0矛盾.故假设不成立.
双曲线的焦点只能在x轴上.
故选A.

练习册系列答案
相关题目
已知椭圆C: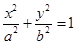
 的离心率为
的离心率为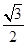 ,过右焦点
,过右焦点 且斜率为
且斜率为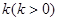 的直线与椭圆C相交于
的直线与椭圆C相交于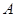 、
、 两点.若
两点.若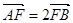 ,则
,则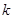 =( )
=( )
A. | B.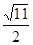 | C.2 | D. |
如果椭圆 的弦被点(4,2)平分,则这条弦所在的直线方程是 ( )
的弦被点(4,2)平分,则这条弦所在的直线方程是 ( )
A.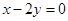 | B.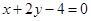 |
C. | D.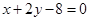 |
已知双曲线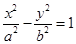 的一条渐近线方程为
的一条渐近线方程为 ,则该双曲线的离心率为
,则该双曲线的离心率为
A.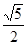 | B.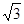 | C.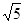 | D.2 |
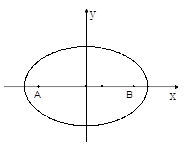
椭圆满足这样的光学性质:从椭圆的一个焦点发射的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.现有一个水平放置的椭圆形台球盘,满足方程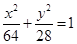 ,点
,点 是它的两个焦点.当静止的小球从点
是它的两个焦点.当静止的小球从点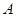 开始出发,沿直线运动,经椭圆壁反射后再回到点
开始出发,沿直线运动,经椭圆壁反射后再回到点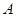 时,此时小球经过的路程可能是 ( )
时,此时小球经过的路程可能是 ( )
A.32或4或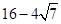 | B.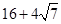 或28或 或28或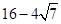 |
C.28或4或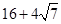 | D.32或28或4 |
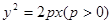 的焦点F且倾斜角为60°的直线l与抛物线在第一、四象限分别交于A、B两点,则
的焦点F且倾斜角为60°的直线l与抛物线在第一、四象限分别交于A、B两点,则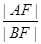 的值等于 ( )
的值等于 ( ) 是抛物线y2=2px(p>0)上的两点,并且满足OA⊥OB. 则y1y2等于
是抛物线y2=2px(p>0)上的两点,并且满足OA⊥OB. 则y1y2等于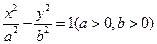 的一条渐近线方程是y=
的一条渐近线方程是y=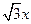 ,它的一个焦点在抛物线
,它的一个焦点在抛物线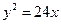 的准线上,则双曲线的方程为( )
的准线上,则双曲线的方程为( )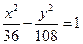 B
B 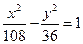
 C
C  D
D