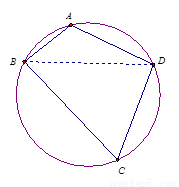
题目内容
(本题满分16分)已知圆 过点
过点 且与圆
且与圆 :
:
 关于直线
关于直线 对称,作斜率为
对称,作斜率为 的直线
的直线 与圆
与圆 交于
交于 两点,且点
两点,且点 在直线
在直线 的左上方。
的左上方。
(1)求圆C的方程。
(2)证明:△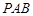 的内切圆的圆心在定直线
的内切圆的圆心在定直线 上。
上。
(3)若∠ ,求△
,求△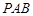 的面积。
的面积。
【答案】
解:(1)设圆心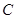
 ,则
,则 , 解得
, 解得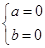 ……………………2分
……………………2分

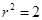 , ∴圆C的方程为
, ∴圆C的方程为 ………………………………………4分
………………………………………4分
(2)设直线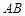 的方程为:
的方程为: ,
,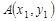 ,
, ,
,
由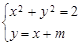 可得:
可得: ,
,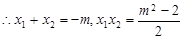
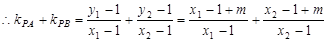
=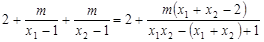
=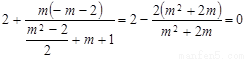
从而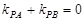 ,因此, ∠
,因此, ∠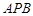 的平分线为垂直于
的平分线为垂直于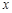 轴的直线,又
轴的直线,又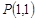 ,所以△
,所以△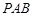 的内切圆的圆心在直线
的内切圆的圆心在直线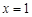 上。………………………………………………10分
上。………………………………………………10分
(3)若∠ ,结合(2)可知:
,结合(2)可知: ,
,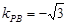 ……………………11分
……………………11分
直线 的方程为:
的方程为: ,圆心
,圆心 到直线
到直线 的距离
的距离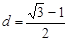
 …………………………………13分
…………………………………13分
同理可得: …………………………………………………………15分
…………………………………………………………15分
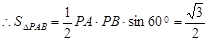 ………………………………………………16分。
………………………………………………16分。
注:(3)解法二: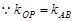
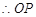 ∥
∥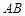 ,
,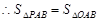 ,又
,又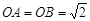 ,
,
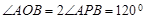 ,
,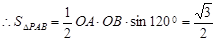
【解析】略

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
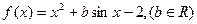 ,且对任意
,且对任意 ,有
,有 .
. ;
;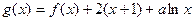 在区间(0,1)上为单调函数,求实
在区间(0,1)上为单调函数,求实 数
数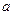 的取值范围.
的取值范围. 的零点个数?(提示
的零点个数?(提示 )
)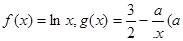 为实常数).
为实常数).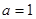 时,求函数
时,求函数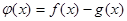 在
在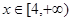 上的最小值;
上的最小值;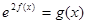 在区间
在区间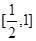 上有解,求实数
上有解,求实数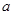 的取值范围;
的取值范围;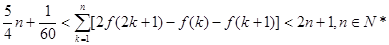
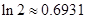 )
)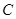 :
: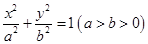 的离心率为
的离心率为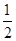 ,
, 分别为椭圆
分别为椭圆 为椭圆上任意一点,以
为椭圆上任意一点,以 为半径作圆
为半径作圆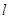 有公共点时,求△
有公共点时,求△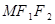 面积的最大值.
面积的最大值.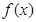 是定义在
是定义在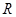 上的偶函数,且当
上的偶函数,且当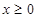 时,
时,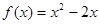 。
。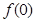 及
及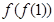 的值;
的值; 上的解析式;
上的解析式;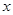 的方程
的方程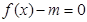 有四个不同的实数解,求实数
有四个不同的实数解,求实数 的取值范围。
的取值范围。