题目内容
已知向量 ,
, ,
, ,
,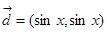 .
.
(1)当 时,求向量
时,求向量 与
与 的夹角
的夹角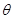 ;
;
(2)当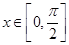 时,求
时,求 的最大值;
的最大值;
(3)设函数 ,将函数
,将函数 的图像向右平移
的图像向右平移 个长度单位,向上平移
个长度单位,向上平移 个长度单位
个长度单位 后得到函数
后得到函数 的图像,且
的图像,且 ,令
,令 ,求
,求 的最小值.
的最小值.
(1)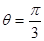 ;(2)
;(2)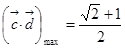 ;(3)
;(3)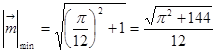 .
.
解析试题分析:(1)根据已知 代入
代入 ,
, ,得到
,得到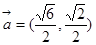 和
和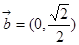 ,由向量的数量积公式
,由向量的数量积公式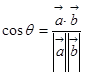 即可求出夹角的余弦值,进而得到向量
即可求出夹角的余弦值,进而得到向量 与
与 的夹角
的夹角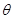 ;
;
(2)根据向量的数量积的坐标运算化简 得,
得,
 ,然后由
,然后由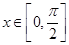 确定
确定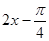 的取值范围,最后由正弦函数图像与性质确定其最大值;
的取值范围,最后由正弦函数图像与性质确定其最大值;
(3)首先根据向量的数量积运算性质得到函数 的解析式即
的解析式即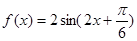 ,然后根据正弦函数的平移规律得到
,然后根据正弦函数的平移规律得到 的解析式即
的解析式即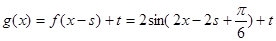 ,再由题意
,再由题意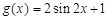 得,
得,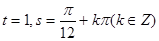 ,进而得到
,进而得到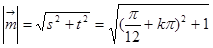 ,易知其最小值.
,易知其最小值.
试题解析:(1)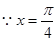 ,
,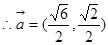 ,
, 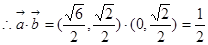
而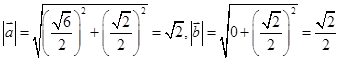
 ,即
,即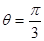 .
.
(2)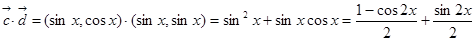

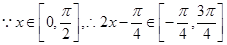
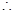 当
当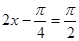 ,即
,即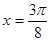 ,
,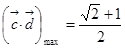 .
.
(3)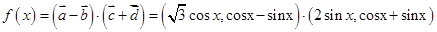
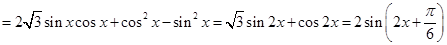
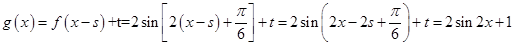
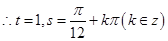
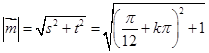
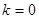 时,
时,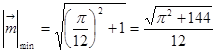 .
.
考点:三角函数中的恒等变换应用;平面向量数量积的运算;三角函数的图象与性质.

练习册系列答案
相关题目
 的值为________.
的值为________. ,
, .
. ,求
,求 ;
; 与
与 垂直,求当
垂直,求当 为何值时,
为何值时, .
. 满足|
满足| |=|
|=| |=1,且|2
|=1,且|2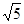 .
. 的值;
的值;  与
与 夹角
夹角 .
. ,
, , 且
, 且
 的解析式;
的解析式; 时,
时,  的值.
的值.
 ,求x的范围;
,求x的范围; 的最大值以及此时x的值.
的最大值以及此时x的值. :
: 的焦点为
的焦点为 ,若过点
,若过点 的直线与抛物线相交于
的直线与抛物线相交于 两点,且
两点,且 .
. 为抛物线
为抛物线 ,
, 为
为 的最小值.
的最小值. ,
, ,(1)若
,(1)若 与
与 垂直,求
垂直,求 的值;(2)若
的值;(2)若 ,求
,求 ,
, ,
, 为锐角.
为锐角. ,求
,求 的值;
的值; ,求
,求 的值.
的值.