题目内容
已知向量a与向量b的夹角为120°,若向量c=a+b,且a⊥c,则 的值为________.
的值为________.
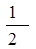
解析试题分析:根据题意可知a⊥c,则可知a c=0,那么a
c=0,那么a c= a
c= a (a+b)=0,即为a
(a+b)=0,即为a a+a
a+a b=0
b=0
因为向量a与向量b的夹角为120°,故有a2+|a||b|cos1200=0,可以解得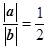 ,故填写
,故填写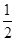 。
。
考点:本试题主要考查了向量的数量积的运算的运用,考查向量的模长的比值。
点评:把向量的垂直问题转化为数量积为0是解决问题的关键,属中档题.

练习册系列答案
相关题目
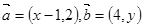 ,若
,若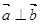 ,则
,则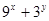 的最小值为 。
的最小值为 。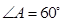 ,D是AB的中点,则
,D是AB的中点,则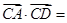 ______.
______. ,则λ=_____________.
,则λ=_____________. ,
, ,
, ,
,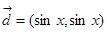 .
. 时,求向量
时,求向量 与
与 的夹角
的夹角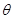 ;
;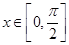 时,求
时,求 的最大值;
的最大值; ,将函数
,将函数 的图像向右平移
的图像向右平移 个长度单位,向上平移
个长度单位,向上平移 个长度单位
个长度单位 后得到函数
后得到函数 的图像,且
的图像,且 ,令
,令 ,求
,求 的最小值.
的最小值. 的最小值是 。
的最小值是 。 、
、 为互相垂直的单位向量,非零向量
为互相垂直的单位向量,非零向量 ,若向量
,若向量 与向量
与向量 、
、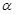 、
、 ,则
,则
 , 则
, 则 = .
= . 为三个非零向量,且
为三个非零向量,且 ,则
,则 的最大值是____▲_____.
的最大值是____▲_____.