题目内容
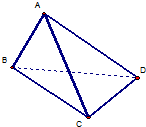 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=| 3 |
(1)求证:AD⊥BC
(2)求二面角B-AC-D的大小.
分析:(1)根据所给的三棱锥中的各边关系,可以判断△BCD为等腰直角三角形,又因为∵△ABC为等边三角,所以若取BC中点O,连AO、DO,则AO⊥BC,DO⊥BC,就可得到BC⊥平面AOD,BC⊥AD.
(2)欲求二面角B-AC-D的大小,先找到二面角的平面角,二面角的平面角满足,顶点在棱上,两条边分别在两个面内,且两条边分别垂直于棱,因为图中没有满足条件的角,所以可以添加辅助线,作BM⊥AC于M,作MN⊥AC交AD于N,
则∠BMN就是二面角B-AC-D的平面角.在把角放入三角形BMN中,通过解三角形求出该角.
(2)欲求二面角B-AC-D的大小,先找到二面角的平面角,二面角的平面角满足,顶点在棱上,两条边分别在两个面内,且两条边分别垂直于棱,因为图中没有满足条件的角,所以可以添加辅助线,作BM⊥AC于M,作MN⊥AC交AD于N,
则∠BMN就是二面角B-AC-D的平面角.在把角放入三角形BMN中,通过解三角形求出该角.
解答:证明:(1)在Rt△ABD与Rt△ACD中,∵AD是公共的斜边,且AD=
,BD=CD=1,∴AB=AC=
∵∵△ABC为等边三角形,∴BC=
,
∴△BCD为等腰直角三角形,
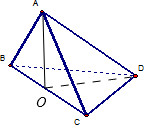 取BC的中点O,连AO、DO,
取BC的中点O,连AO、DO,
∵△ABC为等边三角形,∴AO⊥BC
∵△BCD为等腰直角三角形,∴DO⊥BC.
∴BC⊥平面AOD,∴BC⊥AD.
解:(2)作BM⊥AC于M,作MN⊥AC交AD于N,
则∠BMN就是二面角B-AC-D的平面角.
∵AB=AC=BC=
,M是AC的中点,且MN∥CD
则BM=
,MN=
CD=
,BN=
AD=
.
由余弦定理得cos∠BMN=
=
,
∴∠BMN=arccos
.
| 3 |
| 2 |
∵∵△ABC为等边三角形,∴BC=
| 2 |
∴△BCD为等腰直角三角形,
 取BC的中点O,连AO、DO,
取BC的中点O,连AO、DO,∵△ABC为等边三角形,∴AO⊥BC
∵△BCD为等腰直角三角形,∴DO⊥BC.
∴BC⊥平面AOD,∴BC⊥AD.
解:(2)作BM⊥AC于M,作MN⊥AC交AD于N,
则∠BMN就是二面角B-AC-D的平面角.
∵AB=AC=BC=
| 2 |
则BM=
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |

由余弦定理得cos∠BMN=
| BM2+MN2-BN2 |
| 2BM•MN |
| ||
| 3 |
∴∠BMN=arccos
| ||
| 3 |
点评:本题主要考查立体几何中异面直线垂直的证明,以及二面角的求法,考查了学生的空间想象力,识图能力和转化能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
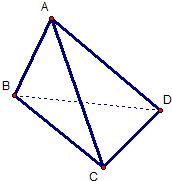 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=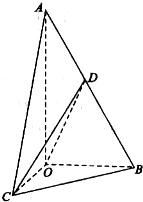 如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,
如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4, 如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC.
如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC. 如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,
如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,