题目内容
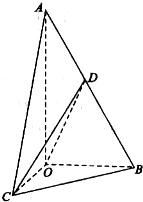 如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=2
如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=2| 2 |
(Ⅰ)求证:平面COD⊥平面AOB;
(Ⅱ)当点D运动到线段AB的中点时,求二面角D-CO-B的大小;
(Ⅲ)当CD与平面AOB所成角最大时,求三棱锥C-OBD的体积.
分析:(Ⅰ)欲证平面COD⊥平面AOB,根据面面垂直的判定定理可知在平面COD内一直线与平面AOB垂直,根据勾股定理可知OC⊥OB,根据线面垂直的判定定理可知OC⊥平面AOB,而OC?平面COD,满足定理所需条件;
(Ⅱ)根据OC⊥OB,OC⊥OD,可知∠DOB是二面角D-CO-B的平面角,在三角形DOB中求出此角即可;
(Ⅲ)根据线面所成角的定义可知∠CDO是CD与平面AOB所成角,然后表示出此角的正切值,再根据正切函数的单调性知,当OD最小时,∠CDO最大,最后根据三棱锥的体积公式求出所求即可.
(Ⅱ)根据OC⊥OB,OC⊥OD,可知∠DOB是二面角D-CO-B的平面角,在三角形DOB中求出此角即可;
(Ⅲ)根据线面所成角的定义可知∠CDO是CD与平面AOB所成角,然后表示出此角的正切值,再根据正切函数的单调性知,当OD最小时,∠CDO最大,最后根据三棱锥的体积公式求出所求即可.
解答:解:
(Ⅰ)证明:∵AO⊥底面BOC,∴AO⊥OC,AO⊥OB.
∵∠OAB=∠OAC=30°,AB=AC=4,∴OC=OB=2.(2分)
∵BC=2
,∴OC⊥OB,∴OC⊥平面AOB.(4分)
∵OC?平面COD,∴平面COD⊥平面AOB.(5分)
(Ⅱ):由(Ⅰ)知OC⊥平面AOB,
∴OC⊥OB,OC⊥OD,
∴∠DOB是二面角D-CO-B的平面角.(7分)
∵D为AB的中点,∴OD=2,BD=2,
又OB=2,∴∠DOB=60°,
∴二面角D-CO-B的大小为60°.(9分)
(Ⅲ):∵OC⊥平面AOB,CD交平面AOB于D,
∴∠CDO是CD与平面AOB所成角.(10分)
tan∠CDO=
=
,据正切函数的单调性知,当OD最小时,∠CDO最大,
∴取OD⊥AB,OD=
为最小值,此时,BD=1.(12分)
∴VC-OBD=
×
×
×1×2=
.
即CD与平面AOB所成角最大时,三棱锥C-OBD的体积为
.(14分)
(Ⅰ)证明:∵AO⊥底面BOC,∴AO⊥OC,AO⊥OB.
∵∠OAB=∠OAC=30°,AB=AC=4,∴OC=OB=2.(2分)
∵BC=2
| 2 |
∵OC?平面COD,∴平面COD⊥平面AOB.(5分)
(Ⅱ):由(Ⅰ)知OC⊥平面AOB,
∴OC⊥OB,OC⊥OD,
∴∠DOB是二面角D-CO-B的平面角.(7分)
∵D为AB的中点,∴OD=2,BD=2,
又OB=2,∴∠DOB=60°,
∴二面角D-CO-B的大小为60°.(9分)
(Ⅲ):∵OC⊥平面AOB,CD交平面AOB于D,
∴∠CDO是CD与平面AOB所成角.(10分)
tan∠CDO=
| OC |
| OD |
| 2 |
| OD |
∴取OD⊥AB,OD=
| 3 |
∴VC-OBD=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |
即CD与平面AOB所成角最大时,三棱锥C-OBD的体积为
| ||
| 3 |
点评:本题主要考查平面与平面垂直的判定,以及二面角的平面角的度量和棱锥体积的求解,同时考查了空间想象能力,计算能力和推理能力,以及转化与划归的思想,属于中档题.

练习册系列答案
相关题目
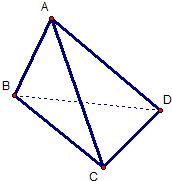 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD= 如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC.
如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC. 如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,
如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,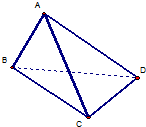 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=