��Ŀ����
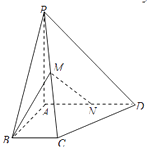
����Ŀ������������е����ʣ���1������֮�ʹ��ڵ����ߣ���2����λ�߳����ڵױߵ�һ�룻��3�����ڽ�ƽ���߽���һ�㣻 �ɵ�������Ķ�Ӧ���ʣ���1����������������֮�ʹ��ڵ��ĸ�����������2����������Ľ���ͬһ�������������е��ƽ��������ڵ��ĸ��������![]() ����3�����������������ǵ�ƽ���潻��һ�㡣�����������������ȷ���� ( )
����3�����������������ǵ�ƽ���潻��һ�㡣�����������������ȷ���� ( )
A. ��1�� B. ��1����2�� C. ��1����2����3�� D. ������
���𰸡�C
��������
���������ֱ�ӵý��۳���.
�����⣬������ƽ���ڡ������ε�����֮�ʹ��ڵ����ߡ�����ڿռ��С����������������������֮�ʹ��ڵ��������������⣨1����ȷ��
��ƽ�漸�����ߵ����ʣ���������ռ伸����������ʣ��ɵù�������Ľ���ͬһ�������������е��ƽ��������ڵ��ĸ��������![]() ����2����ȷ��
����2����ȷ��
��һ����άƽ���ϵ���������Ϊһ����ά�������ϵ���ɵ����������������ǵ�ƽ���潻��һ�㣬��3����ȷ��
��ѡ��C��

 �ŵ������ϵ�д�
�ŵ������ϵ�д� 53������ϵ�д�
53������ϵ�д�����Ŀ����֪ijУ5��ѧ����ĩ������ѧ�ɼ����ܷ��꼶�������±���
ѧ���ı�� | 1 | 2 | 3 | 4 | 5 |
��ѧ | 115 | 112 | 93 | 125 | 145 |
�꼶���� | 250 | 300 | 450 | 70 | 10 |
��1��ͨ��������ʵ֤�����֣�һ��ѧ������ѧ�ɼ����ܷ��꼶�������к�ǿ��������ع�ϵ����������������ȷ��ǰ���£���![]() ��ʾ��ѧ�ɼ�����
��ʾ��ѧ�ɼ�����![]() ��ʾ�꼶��������
��ʾ�꼶��������![]() ��
��![]() �Ļع鷽�̣�������
�Ļع鷽�̣�������![]() ��ȡ������
��ȡ������
��2�����ڱ��ο����У�Ԥ����ѧ����Ϊ120�ֵ�ѧ���꼶��������Ƕ��٣�
�ο����ݺ�ʽ��![]() ������
������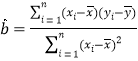 ��
��![]() ������
������![]()