题目内容
把边长为6的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为x,容积为V(x).
(1)写出函数V(x)的解析式,并求出函数的定义域;
(2)求当x为多少时,容器的容积最大?并求出最大容积.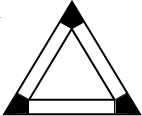
(1)写出函数V(x)的解析式,并求出函数的定义域;
(2)求当x为多少时,容器的容积最大?并求出最大容积.

(1)因为容器的高为x,则做成的正三棱柱形容器的底边长为(6-2
x)(1分).
则V(x)=
(6-2
x)2x(4分)
函数的定义域为(0,
)(5分)
(2)实际问题归结为求函数V(x)在区间(0,
)上的最大值点.先求V(x)的极值点.
在开区间(0,
)内,V′(x)=9
x2-36x+9
(7分)
令V′(x)=0,即令9
x2-36x+9
=0,解得x1=
,x2=
(舍去).
因为x1=
在区间(0,
)内,x1可能是极值点.当0<x<x1时,V′(x)>0;
当x1<x<
时,V′(x)<0.(9分)
因此x1是极大值点,且在区间(0,
)内,x1是唯一的极值点,
所以x=x1=
是V(x)的最大值点,并且最大值 f(
)=4
即当正三棱柱形容器高为
时,容器的容积最大为4.
| 3 |
则V(x)=
| ||
| 4 |
| 3 |
函数的定义域为(0,
| 3 |
(2)实际问题归结为求函数V(x)在区间(0,
| 3 |
在开区间(0,
| 3 |
| 3 |
| 3 |
令V′(x)=0,即令9
| 3 |
| 3 |
| ||
| 3 |
| 3 |
因为x1=
| ||
| 3 |
| 3 |
当x1<x<
| 3 |
因此x1是极大值点,且在区间(0,
| 3 |
所以x=x1=
| ||
| 3 |
| ||
| 3 |
即当正三棱柱形容器高为
| ||
| 3 |

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 以下。
以下。