题目内容
已知向量 ,
, 满足|
满足| |="2," |
|="2," |  |=l,且(
|=l,且( +
+ )⊥(
)⊥(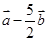 ),则
),则 与
与 的夹角为
的夹角为
A.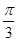 | B.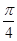 | C.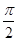 | D.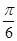 |
A
解析试题分析:因为( +
+ )⊥(
)⊥(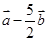 ),所以(
),所以( +
+ )(
)(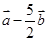 )=0,化为
)=0,化为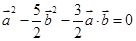 ,又因为|
,又因为| |="2," |
|="2," |  |=l,所以
|=l,所以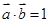 ,求得
,求得 与
与 的夹角为
的夹角为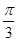 。故选A。
。故选A。
考点:向量的数量积;向量垂直的条件
点评:本题用到向量垂直的结论: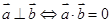 。在向量中,还有另一个重要的结论:
。在向量中,还有另一个重要的结论: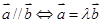 。
。

练习册系列答案
相关题目
对任意两个非零的平面向量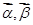 ,定义
,定义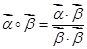 .若平面向量
.若平面向量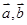 满足
满足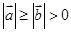 ,
,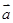 与
与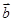 的夹角
的夹角 ,且
,且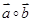 和
和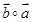 都在集合
都在集合 中,则
中,则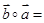 ( )
( )
A. | B. | C.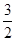 | D. |
已知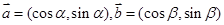 则 ( )
则 ( )
A.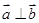 | B.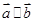 |
C.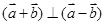 | D.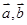 的夹角为 的夹角为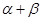 |
设e1,e2是两个互相垂直的单位向量,且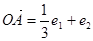 ,
,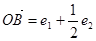 则
则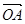 在
在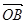 上的投影为( )
上的投影为( )
A.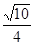 | B.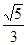 | C.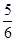 | D.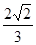 |
正方形ABCD的边长为1,记 =
=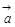 ,
,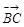 =
=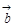 ,
, =
=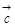 ,则下列结论错误的是( )
,则下列结论错误的是( )
A.(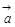 - -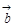 )· )·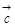 =0 =0 | B.(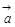 + +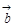 - -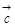 )· )·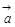 =0 =0 |
C.(|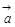 - -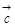 | -| | -|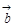 |) |)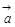 = =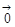 | D.|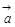 + +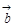 + +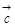 |= |= |
若向量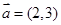 ,
,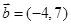 ,则
,则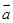 在
在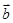 方向上的投影为( )
方向上的投影为( )
A.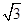 | B.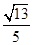 | C.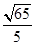 | D.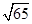 |
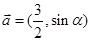 ,
,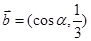 ,且
,且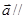
 ,则锐角
,则锐角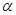 为
为
A. | B.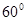 | C. | D.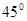 |
在平面内有DABC和点O,若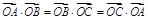 ,则点O是DABC的( )
,则点O是DABC的( )
| A.重心 | B.垂心 | C.内心 | D.外心 |
已知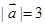 ,
, 在
在 方向上的投影为
方向上的投影为 ,则
,则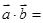
| A.3 | B.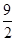 | C.2 | D.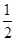 |