题目内容
对任意两个非零的平面向量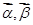 ,定义
,定义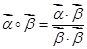 .若平面向量
.若平面向量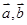 满足
满足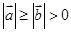 ,
,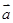 与
与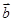 的夹角
的夹角 ,且
,且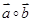 和
和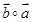 都在集合
都在集合 中,则
中,则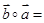 ( )
( )
A. | B. | C.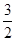 | D. |
A
解析试题分析:由题意可得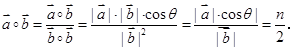
同理可得 
由于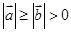 ,所以,
,所以,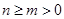 且
且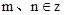 .
.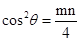 .
.
再由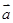 与
与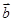 的夹角
的夹角 ,可得
,可得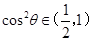 ,即
,即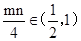 .
.
故有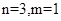 ,
,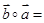
 ,故选A.
,故选A.
考点:平面向量的“新定义”运算

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图,在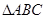 中,
中,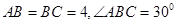 ,AD是边BC上的高,则
,AD是边BC上的高,则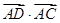 的值等于( )
的值等于( )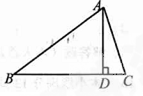
| A.0 | B.4 | C.8 | D.-4 |
已知向量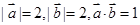 ,则向量
,则向量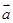 与
与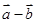 的夹角为( )
的夹角为( )
A.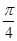 | B.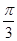 | C.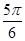 | D.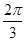 |
已知向量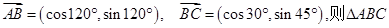 的形状为( )
的形状为( )
| A.直角三角形 | B.等腰三角形 | C.锐角三角形 | D.钝角三角形 |
已知向量 ,且
,且 ,则
,则 等于( )
等于( )
A. | B.0 | C. | D. |
已知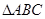 的外接圆半径为1,圆心为O,且
的外接圆半径为1,圆心为O,且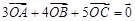 ,则
,则 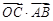 的值为( )
的值为( )
A.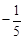 | B.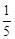 | C.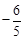 | D.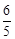 |
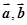 是两个向量,
是两个向量,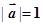 ,
,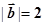 ,且
,且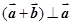 ,则
,则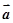 与
与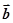 的夹角为( )
的夹角为( )
A.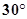 | B. | C.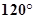 | D.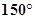 |
已知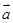 、
、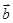 是平面向量,若
是平面向量,若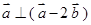 ,
,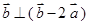 ,则
,则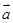 与
与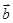 的夹角是( )
的夹角是( )
A.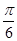 | B.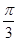 | C.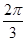 | D.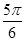 |
已知向量 ,
, 满足|
满足| |="2," |
|="2," |  |=l,且(
|=l,且( +
+ )⊥(
)⊥(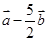 ),则
),则 与
与 的夹角为
的夹角为
A.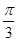 | B.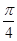 | C.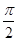 | D.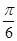 |