Question

已知圆O：x²+y²=1，O为坐标原点，若正方形ABCD的一边AB为圆O的一条弦，则线段OC长度的最大值是________．

Answer 1

+1
分析：设正方形边长为a，∠OBA=θ，从而在△OBC中，计算OC的长，利用三角函数，可求OC的最大值．
解答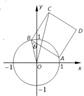：如图，设正方形边长为a，∠OBA=θ，则cosθ=，θ∈[0，）．
在△OBC中，a²+1-2acos（+θ）=OC²，
∴OC²=（2cosθ）²+1+2•2cosθ•sinθ=4cos²θ+1+2sin2θ=2cos2θ+2sin2θ+3=2sin（2θ+）+3，
∵θ∈[0，），
∴2θ+∈[，），
∴2θ+=时，OC²的最大值为2+3
∴线段OC长度的最大值是+1
故答案为：+1
点评：本题考查直线与圆的位置关系，考查三角函数的化简，解题的关键是构建OC关于θ的三角函数，属于中档题．