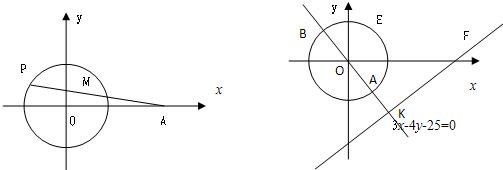
题目内容
已知圆O:x2+y2=9,定点 A(6,0),直线l:3x-4y-25=0
(1)若P为圆O上动点,求线段PA的中点M的轨迹方程
(2)设E、F分别是圆O和直线l上任意一点,求线段EF的最小值.

(1)若P为圆O上动点,求线段PA的中点M的轨迹方程
(2)设E、F分别是圆O和直线l上任意一点,求线段EF的最小值.

分析:(1)利用M是线段PA的中点,寻找动点与定点之间的关系,借助于P在圆O上,从而求出M的轨迹方程
(2)根据图形易知,当且仅当过圆心垂直于已知直线时取得最大与最小值.
(2)根据图形易知,当且仅当过圆心垂直于已知直线时取得最大与最小值.
解答:(1)解:设圆O上动点P(x1,y1),线段PA的中点M(x,y)
由P在圆O上,得x12+y12=9,…(I)
又M是线段PA的中点,则
,∴
∴P(2x-6,2y)
将P点坐标代入(I)得:(2x-6)2+(2y)2=9,
故;(x-3)2+(y)2=
是所求的轨迹方程.
(2)解:过点O作直线OK⊥l于K,交圆O于A、B两点(如图2)|EF|min=|AK|=|OK|-|OA|=5-3=2
由P在圆O上,得x12+y12=9,…(I)
又M是线段PA的中点,则
|
|
将P点坐标代入(I)得:(2x-6)2+(2y)2=9,
故;(x-3)2+(y)2=
| 9 |
| 4 |
(2)解:过点O作直线OK⊥l于K,交圆O于A、B两点(如图2)|EF|min=|AK|=|OK|-|OA|=5-3=2

点评:本题主要考查代入法求轨迹,考查数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
 已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为
已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为 已知圆o:x2+y2=b2与椭圆
已知圆o:x2+y2=b2与椭圆