题目内容
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.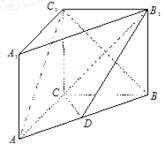
(1)求证: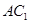 ∥平面
∥平面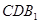 ;
;
(2)求异面直线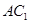 与
与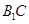 所成角的余弦值.
所成角的余弦值.
(1)证明见解析;(2)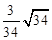 .
.
解析试题分析:(1)设BC1与CB1交于点O,连接OD,利用三角形中位线性质,证明OD∥AC1,利用线面平行的判定,可得AC1∥平面CDB1;(2)过C作CE⊥AB于E,连接C1E,证明∠CEC1为二面角C1-AB-C的平面角,从而可求二面角C1-AB-C的余弦值.
试题解析:(1)证明:设BC1与CB1交于点O,则O为BC1的中点,
在△ABC1中,连接OD,
∵D,O分别为AB,BC1的中点,
∴OD为△ABC1的中位线,
∴OD∥AC1,
又∵AC1Ú平面CDB1,OD?平面CDB1,
∴AC1∥平面CDB1;
(2)解:过C作CE⊥AB于E,连接C1E,
∵CC1⊥底面ABC,
∴C1E⊥AB,
∴∠CEC1为二面角C1-AB-C的平面角,
在△ABC中,AC=3,BC=4,AB=5,
∴CE= ,
,
在Rt△CC1E中,tan∠C1EC=4: =
=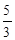 ,
,
∴cos∠C1EC=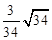 ,
,
∴二面角C1-AB-C的余弦值为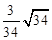 .
.
考点: 1.直线与平面平行的判定;2.二面角的平面角及求法.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 中,
中, ,点
,点 分别是
分别是 的中点,将
的中点,将 分别沿
分别沿 折起,使
折起,使 两点重合于点
两点重合于点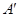 .
.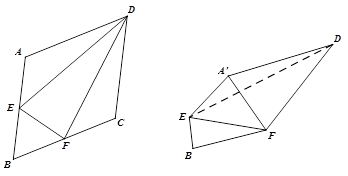 (1)求证:
(1)求证: ;
; 的余弦值.
的余弦值. ,
, ,DC=1,AB=2,PA⊥平面ABCD,PA=1.
,DC=1,AB=2,PA⊥平面ABCD,PA=1.
 中,
中,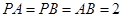 ,
, ,
, °,平面
°,平面 平面
平面 ,
, 、
、 分别为
分别为 、
、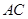 中点.
中点.
 ∥平面
∥平面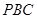 ;
; ;
; 的大小.
的大小.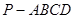 中,底面
中,底面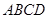 为梯形,
为梯形,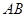 ∥
∥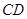 ,
, 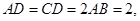
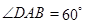 ,
,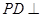 平面
平面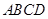 ,
,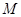 为
为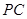 的中点
的中点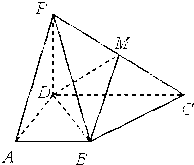
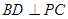
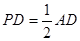 ,求二面角
,求二面角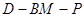 的余弦值
的余弦值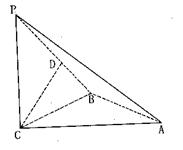
 的底面
的底面 为矩形,且
为矩形,且 ,
,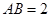 ,
, ,
,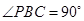 ,
,
 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD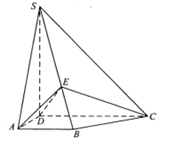
 ;
; ,当平面EDC
,当平面EDC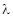 的值;
的值;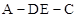 的大小.
的大小.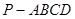 中,底面
中,底面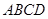 是直角梯形,
是直角梯形,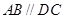 ,
,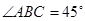 ,
,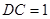 ,
,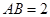 ,
,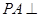 平面
平面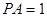 .
. 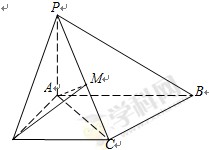
 平面
平面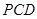 ;
; 平面
平面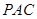 ;
; 是
是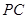 的中点,求三棱锥
的中点,求三棱锥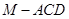 的体积.
的体积.