题目内容
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形, ,
, ,DC=1,AB=2,PA⊥平面ABCD,PA=1.
,DC=1,AB=2,PA⊥平面ABCD,PA=1.
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
(1)证明见解析;
(2)证明:见解析.
解析试题分析:(1)由直线与平面平行的判定定理即得.
(2)注意到在直角梯形ABCD中,过C作CE⊥AB于点E,四边形ADCE为矩形
利用勾股定理计算三角形的边长,进一步得到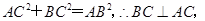 再根据
再根据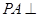 平面
平面 ,即可得出
,即可得出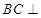 平面
平面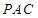 .
.
试题解析:(1)证明: 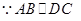 ,且
,且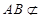 平面
平面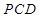 ,
,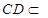 平面
平面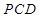 .∴
.∴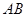 ∥平面
∥平面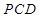 . 5分
. 5分
(2)证明:在直角梯形ABCD中,过C作CE⊥AB于点E,则四边形ADCE为矩形
∴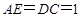 ,又
,又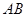
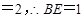 ,在
,在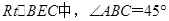 ,
,
所以 ,则
,则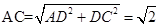 ,
,
∴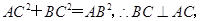 9分
9分
又∵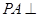 平面
平面 ,
,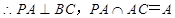 ,∴
,∴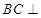 平面
平面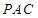 12分
12分
考点:直线与平面平行,勾股定理,垂直关系.

练习册系列答案
相关题目
 中,点
中,点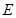 为边
为边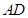 上的点,点
上的点,点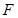 为边
为边 的中点,
的中点, ,现将
,现将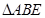 沿
沿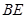 边折至
边折至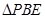 位置,且平面
位置,且平面 平面
平面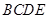 .
.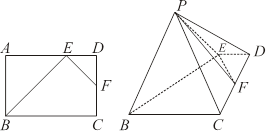
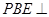 平面
平面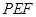 ;
;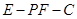 的大小.
的大小.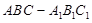 中,
中,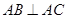 ,
,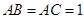 ,
,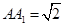 ,D为BC中点.
,D为BC中点.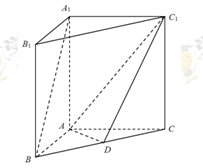
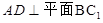 ;
; ;
;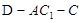 的正弦值.
的正弦值.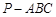 中,点
中,点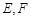 分别是棱
分别是棱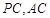 的中点.
的中点.
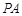 //平面
//平面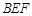 ;
;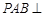 平面
平面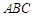 ,
,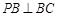 ,求证:
,求证: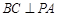 .
. ,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.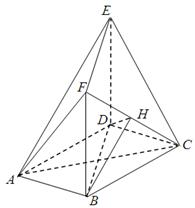
 所成角的正弦值;
所成角的正弦值; 的大小.
的大小. 、
、 、
、 为不在同一直线上的三点,且
为不在同一直线上的三点,且 ,
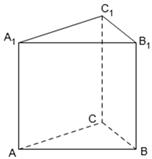
,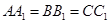 .
.
 //平面
//平面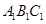 ;
;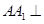 平面
平面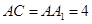 ,
,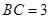 ,
,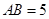 ,求证:
,求证: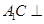 平面
平面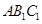 ;
;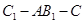 的余弦值.
的余弦值.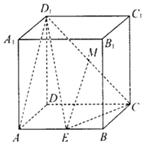
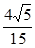 .求线段AE的长.
.求线段AE的长.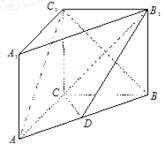
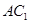 ∥平面
∥平面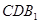 ;
;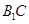 所成角的余弦值.
所成角的余弦值.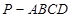 中,底面为直角梯形,
中,底面为直角梯形,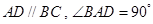 ,
,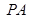 垂直于底面
垂直于底面 ,
,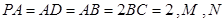 分别为
分别为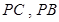 的中点.
的中点.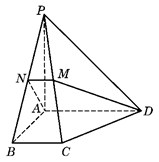
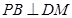 ;
;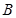 到平面
到平面 的距离.
的距离.