题目内容
20.若按右侧算法流程图运行后,输出的结果是$\frac{5}{6}$,则输入的N的值可以等于( )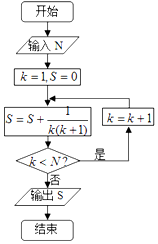
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 模拟执行程序框图,依次写出每次循环得到的K,S的值,由题意,当K=5,S=$\frac{5}{6}$时应该不满足条件K<N,退出循环,输出S的值为$\frac{5}{6}$,即可得解.
解答 解:模拟执行程序框图,可得
K=1,S=0,
第1次循环,S=$\frac{1}{2}$,
满足条件K<N,K=2,S=$\frac{2}{3}$,
满足条件K<N,K=3,S=$\frac{3}{4}$,
满足条件K<N,K=4,S=$\frac{4}{5}$,
满足条件K<N,K=5,S=$\frac{5}{6}$,
由题意,此时应该不满足条件K<N,退出循环,输出S的值为$\frac{5}{6}$,
故输入的N的值可以等于5.
故选:B.
点评 本题主要考察了循环结构的程序框图,正确写出每次循环得到的K,S的值判断循环退出的条件是解题的关键,属于基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.执行如图所示的程序框图,则输出的S值是( )


| A. | $\frac{4}{9}$ | B. | $\frac{17}{18}$ | C. | $\frac{17}{38}$ | D. | $\frac{15}{34}$ |
15.已知数列{an}为等差数列,前n项和为Sn,若a7+a8+a9=$\frac{π}{3}$,则cosS15的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |
5.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)与抛物线y2=2px(p>0)有相同的焦点,且双曲线的一条渐近线与抛物线的准线交于点$(-5,-\frac{15}{4})$,则双曲线的离心率为( )
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{2}$ |
9.执行如图的程序框图,若输入x=1,则输出的S=( )


| A. | 21 | B. | 37 | C. | 57 | D. | 62 |
10.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$的焦距为10,点P(2,1)在C的渐近线上,则C的方程为( )
| A. | $\frac{{x}^{2}}{20}-\frac{{y}^{2}}{5}=1$ | B. | $\frac{{x}^{2}}{5}-\frac{{y}^{2}}{20}=1$ | C. | $\frac{{x}^{2}}{80}-\frac{{y}^{2}}{20}=1$ | D. | $\frac{{x}^{2}}{20}-\frac{{y}^{2}}{80}=1$ |