题目内容
15.已知数列{an}为等差数列,前n项和为Sn,若a7+a8+a9=$\frac{π}{3}$,则cosS15的值为( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |
分析 由题意和等差数列的性质可得a8=$\frac{π}{9}$,进而可得S15=$\frac{5π}{3}$,计算余弦值可得.
解答 解:由等差数列的性质可得3a8=a7+a8+a9=$\frac{π}{3}$,∴a8=$\frac{π}{9}$,
∴S15=$\frac{15({a}_{1}+{a}_{15})}{2}$=$\frac{15×2{a}_{8}}{2}$=15a8=$\frac{5π}{3}$,
∴cosS15=cos$\frac{5π}{3}$=cos$\frac{π}{3}$=$\frac{1}{2}$
故选:B
点评 本题考查等差数列的求和公式和等差数列的性质,涉及三角函数的运算,属基础题.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
10.下列四个命题中正确的命题是( )
| A. | “x>2”是“x>1”的必要不充分条件 | |
| B. | “log2a>log2b”是“a>b”必要不充分条件 | |
| C. | “a≥0”是“a2≤a”的必要不充分条件 | |
| D. | “log2x<0”是“($\frac{1}{2}$)x-1>1”的必要不充分条件 |
7.一个几何体的三视图如图,则该几何体的体积为( )


| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
4. 随着经济发展带来的环境问题,我国很多城市提出了大力发展城市公共交通的理念,同时为了保证不影响市民的正常出行,就要求对公交车的数量必须进行合理配置.为此,某市公交公司在某站台随机对20名乘客进行了调查,其已候车时间情况如表(单位:分钟)
随着经济发展带来的环境问题,我国很多城市提出了大力发展城市公共交通的理念,同时为了保证不影响市民的正常出行,就要求对公交车的数量必须进行合理配置.为此,某市公交公司在某站台随机对20名乘客进行了调查,其已候车时间情况如表(单位:分钟)
(1)画出已候车时间的频率分布直方图
(2)求这20名乘客的平均候车时间
(3)在这20名乘客中随机抽查一人,求其已候车时间不少于15分钟的概率.
 随着经济发展带来的环境问题,我国很多城市提出了大力发展城市公共交通的理念,同时为了保证不影响市民的正常出行,就要求对公交车的数量必须进行合理配置.为此,某市公交公司在某站台随机对20名乘客进行了调查,其已候车时间情况如表(单位:分钟)
随着经济发展带来的环境问题,我国很多城市提出了大力发展城市公共交通的理念,同时为了保证不影响市民的正常出行,就要求对公交车的数量必须进行合理配置.为此,某市公交公司在某站台随机对20名乘客进行了调查,其已候车时间情况如表(单位:分钟)| 组别 | 已候车时间 | 人数 |
| Ⅰ | [0,5) | 4 |
| Ⅱ | [5,10) | 6 |
| Ⅲ | [10,15) | 6 |
| Ⅳ | [15,20) | 3 |
| Ⅴ | [20,25] | 1 |
(2)求这20名乘客的平均候车时间
(3)在这20名乘客中随机抽查一人,求其已候车时间不少于15分钟的概率.
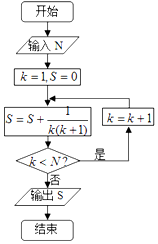
5.执行如图所示的程序框图,要使输出的S的值小于1,则输入的t值不能是下面的( )


| A. | 8 | B. | 9 | C. | 10 | D. | 11 |