题目内容
已知tan(α+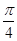 )=-3,α∈(0,
)=-3,α∈(0,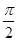 ).
).
(1)求tanα的值;
(2)求sin(2α-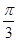 )的值.
)的值.
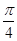 )=-3,α∈(0,
)=-3,α∈(0,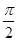 ).
).(1)求tanα的值;
(2)求sin(2α-
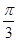 )的值.
)的值.(1)2 (2)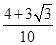
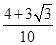
试题分析:(1)由tan(α+
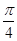 )=-3可得
)=-3可得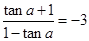
解得tanα=2.
(2)由tanα=2,α∈(0,
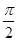 ),可得sinα=
),可得sinα= ,cosα=
,cosα=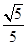 .
.因此sin2α=2sinαcosα=
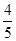 ,cos2α=1-2sin2α=-
,cos2α=1-2sin2α=-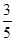 ,
,sin(2α-
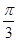 )=sin2αcos
)=sin2αcos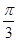 -cos2αsin
-cos2αsin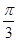 =
=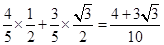
点评:主要是考查了二倍角公式以及两角和差的公式的运用,属于基础题。

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 个单位,沿y轴向下平移1个单位,得到函数y=
个单位,沿y轴向下平移1个单位,得到函数y= sinx的图象则y=f(x)是( )
sinx的图象则y=f(x)是( )
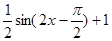


 的图象上每一点向右平移
的图象上每一点向右平移 个单位,再将所得图象上每一点的横坐标扩大为原来的
个单位,再将所得图象上每一点的横坐标扩大为原来的 倍(纵坐标保持不变),得函数
倍(纵坐标保持不变),得函数 的图象,则
的图象,则 的一个解析式为__________________.
的一个解析式为__________________. 分别为三个内角
分别为三个内角 的对边,锐角
的对边,锐角 满足
满足 . (Ⅰ)求
. (Ⅰ)求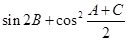 的值;
的值; ,当
,当 取最大值时,求
取最大值时,求 的值.
的值. 在
在 上的最大值
上的最大值 的值。
的值。 ,其图象过点
,其图象过点
 的值;
的值; 图象上各点向左平移
图象上各点向左平移 个单位长度,得到函数
个单位长度,得到函数 的图象,求函数
的图象,求函数 在
在 上的单调递增区间.
上的单调递增区间.
 化简成
化简成 的形式;
的形式; 上的最大值和最小值.
上的最大值和最小值. 的终边上有一点
的终边上有一点 ,则
,则 的值是
的值是 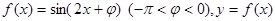 图像的一条对称轴是直线
图像的一条对称轴是直线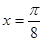 .
.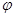 ;(2)画出函数
;(2)画出函数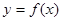 在区间
在区间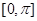 上的图像(在答题纸上完成列表并作图).
上的图像(在答题纸上完成列表并作图).