题目内容

如图，
OA
=
a
，
OB
=
b
，且BC⊥OA于C，设
OC
=λ 
a
，则λ等于（　　）
分析：由
OA
=
a
，
OB
=
b
，
OC
=λ 
a
，知
CB
=
OB
-
OC
=
b
-λ
a
，由BC⊥OA于C，知
CB
•
OA
=(
b
-λ
a
)•
a

=
a
•
b
-λ
a
2=0，由此能求出λ=
a
•
b
|
a
 |2
．
解答：解：∵
OA
=
a
，
OB
=
b
，
OC
=λ 
a
，
∴
CB
=
OB
-
OC
=
b
-λ
a
，
∵BC⊥OA于C，
∴
CB
•
OA
=(
b
-λ
a
)•
a

=
a
•
b
-λ
a
2=0，
∴λ=
a
•
b
|
a
 |2
．
故选A．
点评：本题考查向量在几何中的应用，解题时要认真审题，仔细解答，注意平面向量的数量积的灵活运用．
练习册系列答案
相关题目
如图所示，在△OAB中，OA＞OB，OC=OB，设
OA
=
a
，
OB
=
b
，若
AC
=λ•
AB
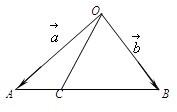
，则实数λ的值为（　　）精英家教网
A、
a
•(
a
-
b
)  
|
a
-
b
|
B、
a
•(
a
-
b
)  
|
a
-
b
|2
C、
a
2-
b
2
|
a
-
b
|
D、
a
2-
b
2
|
a
-
b
|2
（2012•深圳一模）（几何证明选讲选做题）如图4，A，B是圆O上的两点，且OA⊥OB，OA=2，C为OA的中点，连接BC并延长交圆O于点D，则CD=
3
5
5
3
5
5
．
（2012•江西）如图，|OA|=2（单位：m），OB=1（单位：m），OA与OB的夹角为
π
6
，以A为圆心，AB为半径作圆弧
BDC
与线段OA延长线交与点C．甲、乙两质点同时从点O出发，甲先以速度1（单位：m/s）沿线段OB行至点B，再以速度3（单位：m/s）沿圆弧
BDC
行至点C后停止；乙以速率2（单位：m/s）沿线段OA行至A点后停止．设t时刻甲、乙所到的两点连线与它们经过的路径所围成图形的面积为S（t）（S（0）=0），则函数y=S（t）的图象大致是（　　）
（2010•孝感模拟）如图，△OAB中，|
OA
|＞|
OB
|，|
OC
|=|
OB
|，设
OA
=a，
OB
=b，若
AC
=λ•
AB
，则实数λ的值为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网