题目内容
已知集合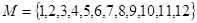 ,以下命题正确的序号是 .
,以下命题正确的序号是 .
①如果函数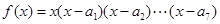 ,其中
,其中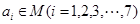 ,那么
,那么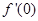 的最大值为
的最大值为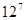 .
.
②数列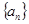 满足首项
满足首项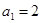 ,
,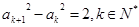 ,当
,当 且
且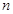 最大时,数列
最大时,数列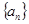 有2048个.
有2048个.
③数列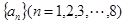 满足
满足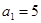 ,
, ,
,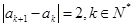 ,如果数列
,如果数列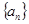 中的每一项都是集合M的元素,则符合这些条件的不同数列
中的每一项都是集合M的元素,则符合这些条件的不同数列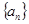 一共有33个.
一共有33个.
④已知直线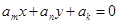 ,其中
,其中 ,而且
,而且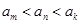 ,则一共可以得到不同的直线196条.
,则一共可以得到不同的直线196条.
②③④
解析试题分析:对①,将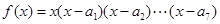 求导得:
求导得: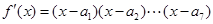
 ,所以
,所以 .故错.
.故错.
对②, 是一个等差数列,
是一个等差数列,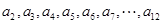 都是互为相反数的两个值,所以数列
都是互为相反数的两个值,所以数列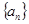 共有
共有 个.
个.
对③,由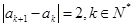 得
得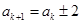 .
.
法一、由于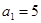 ,
, ,故将
,故将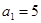 加4个2,再减3个2即可.由于
加4个2,再减3个2即可.由于 故不能连续加4次,也不能连续减3次,所以共有
故不能连续加4次,也不能连续减3次,所以共有 个.
个.
法二、因为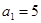 ,所以
,所以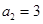 或
或 ,注意到数列
,注意到数列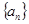 中的每一项都是集合M的元素,依次下去可得
中的每一项都是集合M的元素,依次下去可得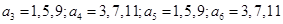 .由于
.由于 ,所以
,所以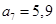 .由此我们可得以下树图:
.由此我们可得以下树图: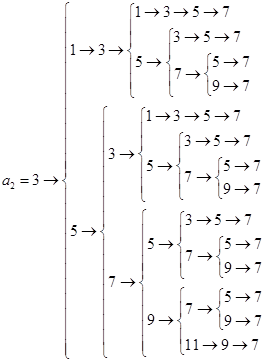 ,
,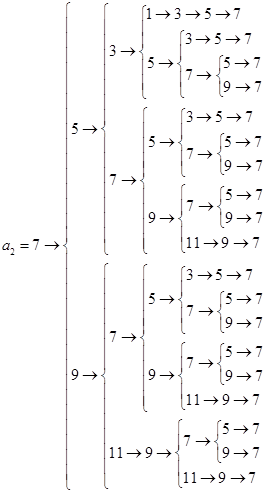
所以符合这些条件的不同数列 一共有14+19=33个.
一共有14+19=33个.
法三、由于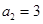 或
或 ,
,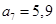 ,故可以分以下四种情况分别求解:
,故可以分以下四种情况分别求解: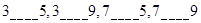 .
. ,共有9个;
,共有9个; ,共有5个;
,共有5个; ,共有10个;
,共有10个; ,共有9个.所以总共有33个.
,共有9个.所以总共有33个.
对④,从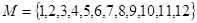 中取3个不同的数作为
中取3个不同的数作为 ,因为
,因为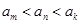 ,所以共有
,所以共有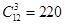 种取法.再排除其中重复的直线.与
种取法.再排除其中重复的直线.与 相同的有
相同的有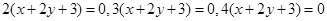 ,多3条;与
,多3条;与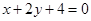 相同的有
相同的有 ,多2条;与
,多2条;与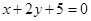 相同的有
相同的有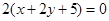 ,多1条;与
,多1条;与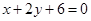 相同的有
相同的有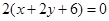 ,多1条;与
,多1条;与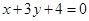 相同的有
相同的有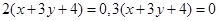 ,多2条;与
,多2条;与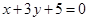 相同的有
相同的有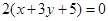 ,多1条;与
,多1条;与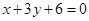 相同的有
相同的有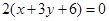 ,多1条;与
,多1条;与 相同的有
相同的有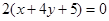 ,多1条;与
,多1条;与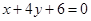 相同的有
相同的有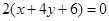 ,多1条;与
,多1条;与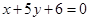 相同的有
相同的有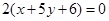 ,多1条;与
,多1条;与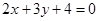 相同的有
相同的有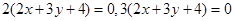 ,多2条;与
,多2条;与 相同的有
相同的有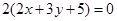 ,多1条;与
,多1条;与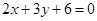 相同的有
相同的有 ,多1条;与
,多1条;与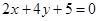 相同的有
相同的有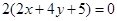 ,多1条;与
,多1条;与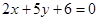 相同的有
相同的有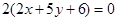 ,多1条(注意
,多1条(注意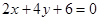 这种情况在前面已经考虑了);与
这种情况在前面已经考虑了);与 相同的有
相同的有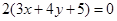 ,多1条;与
,多1条;与
练习册系列答案
相关题目
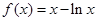 的单调递增区间是
的单调递增区间是 
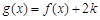 ,若函数
,若函数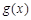 恰有两个不同的零点,则实数
恰有两个不同的零点,则实数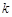 的取值范围为 .
的取值范围为 . ,当变量
,当变量 增加2个单位,其预报值平均增加4个单位;
增加2个单位,其预报值平均增加4个单位; ;
; ,且
,且 ,则
,则 ;
;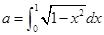 ”是“函数
”是“函数 的最小正周期为4”的充要条件;
的最小正周期为4”的充要条件;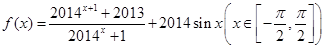 的最大值为M,最小值为m,则M+m=4027,其中正确命题的个数是 个。
的最大值为M,最小值为m,则M+m=4027,其中正确命题的个数是 个。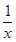 在
在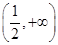 上是增函数,则a的取值范围是________.
上是增函数,则a的取值范围是________.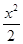 -2x+5,若对任意的x∈[-1,2],都有f(x)>m,则实数m的取值范围为________.
-2x+5,若对任意的x∈[-1,2],都有f(x)>m,则实数m的取值范围为________.