Question

设P（x₀，y₀）是双曲线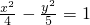的右支上的一点．F₁、F₂分别为左、右焦点，则△PF₁F₂的内切圆的圆心的横坐标为

1. A.
   
2. B.
   3
3. C.
   6
4. D.
   2

Answer 1

D
分析：将内切圆的圆心坐标进行转化成圆与横轴切点Q的横坐标，PF₁-PF₂=F₁Q-F₂Q=4，F₁Q+F₂Q=F₁F₂解出OQ．
解答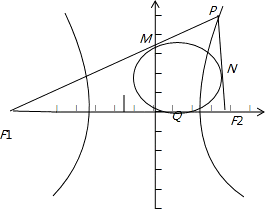：解：如图设切点分别为M，N，Q，则△PF₁F₂的内切圆的圆心的横坐标与Q横坐标相同．
由双曲线的定义，PF₁-PF₂=2a=4．
由圆的切线性质PF₁-PF₂=F_IM-F₂N=F₁Q-F₂Q=4，
∵F₁Q+F₂Q=F₁F₂=6，∴F₂Q=1，OQ=2，Q横坐标为2．
故选D
点评：本题巧妙地借助于圆的切线的性质，强调了双曲线的定义．