题目内容
抛物线的方程是y2=2x,有一个半径为1的圆,圆心在x轴上运动问这个圆运动到什么位置时,圆与抛物线在交点处的切线互相垂直?(注:设P(x0,y0)是抛物线y2=2px上一点,则抛物线在P点处的切线斜率是| P | y0 |
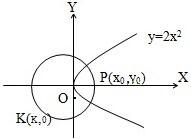
分析:设出圆的方程,再设圆与抛物线的一个交点为P进而可求得在P点圆半径的斜率和在P点抛物线的切线斜率的表达式,根据在P点抛物线的切线与圆的切线垂直,必须且只须圆的半径与抛物线在P点相切进而建立等式,把P点代入抛物线方程和椭圆方程,联立方程组可求得k,则圆的方程可得.
解答:解:设圆的方程为(x-k)2+y2=1
再设圆与抛物线的一个交点为P(x0,y0)
在P点圆半径的斜率=
.
在P点抛物线的切线斜率=
在P点抛物线的切线与圆的切线垂直,必须且只须圆的半径与抛物线在P点相切,
∴
=
.(1)
因P(x0,y0)是圆与抛物线的交点,
∴y02=2x0.(2)
(x0-k)2+y02=1.(3)
由(1)、(2)式消去y0,得x0=-k,
将(2)代入(3),得(x0-k)2+2x0-1=0,
将x0=-k代入,得4k2-2k-1=0,
∴k=
.
由于抛物线在y轴的右方,所以k=-x0≤0
故根号前应取负号,即k=
.故所求圆的方程为(x-
)2+y2=1.
故圆心是(
,0)时圆与抛物线在交点处的切线互相垂直
再设圆与抛物线的一个交点为P(x0,y0)
在P点圆半径的斜率=
| y0 |
| x0-k |
在P点抛物线的切线斜率=
| 1 |
| y0 |
在P点抛物线的切线与圆的切线垂直,必须且只须圆的半径与抛物线在P点相切,
∴
| 1 |
| y0 |
| y0 |
| x0-k |
因P(x0,y0)是圆与抛物线的交点,
∴y02=2x0.(2)
(x0-k)2+y02=1.(3)
由(1)、(2)式消去y0,得x0=-k,
将(2)代入(3),得(x0-k)2+2x0-1=0,
将x0=-k代入,得4k2-2k-1=0,
∴k=
1±
| ||
| 4 |
由于抛物线在y轴的右方,所以k=-x0≤0
故根号前应取负号,即k=
1-
| ||
| 4 |
1-
| ||
| 4 |
故圆心是(
1-
| ||
| 4 |
点评:本题主要考查了圆锥曲线的共同特征.解此类题应充分发挥判别式和韦达定理在解题中的作用.灵活应用数形结合的思想、函数思想、等价转化思想、分类讨论思想解题.

练习册系列答案
相关题目