题目内容
4.a≠0,则y=ax2的焦点坐标和准线方程分别为( )| A. | $(\frac{a}{4},0)$ x=-$\frac{a}{4}$ | B. | $(0,\frac{a}{4})$ y=-$\frac{a}{4}$ | C. | $(\frac{1}{4a},0)$ x=-$\frac{1}{4a}$ | D. | $(0,\frac{1}{4a})$ y=-$\frac{1}{4a}$ |
分析 由条件利用抛物线的标准方程,以及简单性质,分类讨论求出它的焦点坐标和准线方程.
解答 解:当a>0时,抛物线y=ax2(a≠0),
即为x2=$\frac{y}{a}$,
开口向上,2p=$\frac{1}{a}$,$\frac{p}{2}$=$\frac{1}{4a}$,
焦点坐标为(0,$\frac{1}{4a}$),准线方程为y=-$\frac{1}{4a}$.
当a<0时,抛物线y=ax2(a≠0),
即为x2=$\frac{y}{a}$,
开口向下,2p=$\frac{1}{a}$,$\frac{p}{2}$=$\frac{1}{4a}$,
焦点坐标为(0,$\frac{1}{4a}$),准线方程为y=-$\frac{1}{4a}$.
综上可得,抛物线的焦点坐标为(0,$\frac{1}{4a}$),准线方程为y=-$\frac{1}{4a}$.
故选:D.
点评 本题主要考查抛物线的标准方程,以及简单性质的应用,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
14.定义二阶行列式$|\begin{array}{l}{a}&{b}\\{d}&{c}\end{array}|$=ac-bd,那么$|\begin{array}{l}{sin50°}&{cos40°}\\{-\sqrt{3}tan10°}&{1}\end{array}|$=( )
| A. | 1 | B. | -1 | C. | $\sqrt{3}$ | D. | 0 |
12.3名男生与3名女生站在一排,如果要求男女生相间站,那么站法有( )
| A. | 36种 | B. | 72种 | C. | 108种 | D. | 144种 |
13.已知直线y=k(x-2)(k>0)与抛物线y2=8x相交于点A,B两点,F为抛物线的焦点,若|FA|=2|FB|,则k的值为( )
| A. | 4 | B. | 8 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
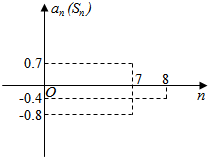 已知等差数列{an}的前n项和为Sn,在同一坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示.
已知等差数列{an}的前n项和为Sn,在同一坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示.