题目内容
已知函数 是在
是在 上每一点均可导的函数,若
上每一点均可导的函数,若 在
在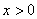 时恒成立.
时恒成立.
(1)求证:函数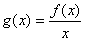 在
在 上是增函数;
上是增函数;
(2)求证:当 时,有
时,有 ;
;
(3)请将(2)问推广到一般情况,并证明你的结论(不要求证明).
【答案】
【解析】(1)由 得
得 因为
因为 ,
,
所以 在
在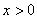 时恒成立,所以函数
时恒成立,所以函数 在
在 上是增函数.……4分
上是增函数.……4分
(2)由(1)知函数 在
在 上是增函数,所以当
上是增函数,所以当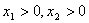 时,
时,
有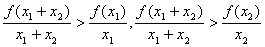 成立, ……6分
成立, ……6分
从而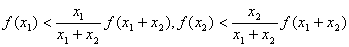 ,
,
两式相加得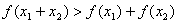 .……8分
.……8分
(3)推广到一般情况为:
若 ,则
,则 ,
,
 . ……12分
. ……12分

练习册系列答案
相关题目
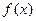 是在
是在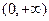 上每一点处均可导的函数,若
上每一点处均可导的函数,若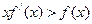 在
在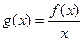 在
在 时,证明:
时,证明: ;
;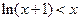 在
在 且
且 时恒成立,求证:
时恒成立,求证: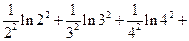 …
…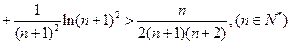
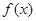 是在
是在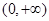 上每一点处均可导的函数,若
上每一点处均可导的函数,若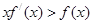 在
在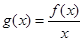 在
在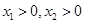 时,证明:
时,证明: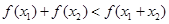 ;
;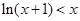 在
在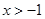 且
且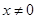 时恒成立,求证:
时恒成立,求证: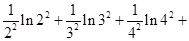 …
…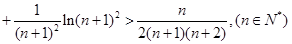
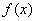 是在
是在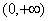 上每一点均可导的函数,若
上每一点均可导的函数,若 在
在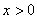 时恒成立.
时恒成立.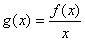 在
在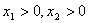 时,有
时,有 ;
;