题目内容
. (本题满分14分)
设命题p:函数 的定义域为R;命题q:
的定义域为R;命题q: 对一切的实数均成立,如果命题“p或q”为真命题,且“p且q”为假命题,求实数a的取值范围。
对一切的实数均成立,如果命题“p或q”为真命题,且“p且q”为假命题,求实数a的取值范围。
解:命题p:∵函数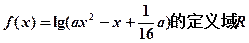
∴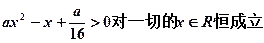
∴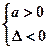 ,即
,即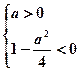 ……………………2分
……………………2分
∴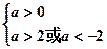 故
故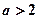 …………………3分
…………………3分
命题q:∵ 对一切的实数均成立
对一切的实数均成立
令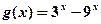 ,则只须
,则只须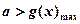 …………4分
…………4分
令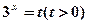 ,则
,则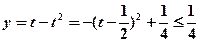
∴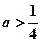 …………………………………7分
…………………………………7分
∵“p或q”为真命题,且“p且q”为假命题,即p与q一真一假
若p真 q假,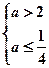 ,无解………………………………………10分
,无解………………………………………10分
若p假q真,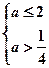 ,∴
,∴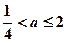 ……………………………13分
……………………………13分
故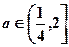 ……………………………………………14分
……………………………………………14分
解析

练习册系列答案
相关题目
已知奇函数f (x)和偶函数g(x)分别满足  ,
,  ,若存在实数a,使得
,若存在实数a,使得  成立,则实数b的取值范围是
成立,则实数b的取值范围是
| A.(-1,1) | B. | C. | D. |
 则
则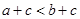 ”. ( 其中
”. ( 其中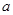 、
、 、
、 )
)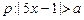 ,(
,(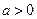 )和条件
)和条件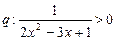 ,
,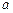 的取值范围,使命题:“
的取值范围,使命题:“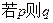 ”为真命题,它的逆命题为假命题。
”为真命题,它的逆命题为假命题。
 |≤2,q:x2-2x+1-m2≤0(m>0),若
|≤2,q:x2-2x+1-m2≤0(m>0),若 p
p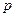 :实数
:实数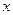 满足
满足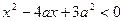 ,其中
,其中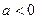 ;
;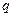 :实数
:实数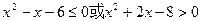 ,且
,且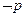 是
是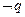 的必要不充分条件,求
的必要不充分条件,求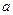 的取值范围。
的取值范围。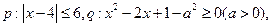 若
若 是
是 的充分不必要条件,求
的充分不必要条件,求 的取值范围
的取值范围  |≤2,q:x2-2x+1-m2≤0(m>0),若
|≤2,q:x2-2x+1-m2≤0(m>0),若 是
是 的必要而不充分条件, 求实数m的取值范围.
的必要而不充分条件, 求实数m的取值范围.  ,设命题
,设命题 函数
函数 为减函数,命题
为减函数,命题 :当
:当 时,函数
时,函数 >
> 恒成立,若
恒成立,若 或
或