题目内容
18. 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,△A1CB是等边三角形,AC=AB=1,B1C1∥BC,BC=2B1C1.
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,△A1CB是等边三角形,AC=AB=1,B1C1∥BC,BC=2B1C1.(Ⅰ)求证:AB1∥平面A1C1C;
(Ⅱ)若点M是边AB上的一个动点(包括A,B两端点),试确定点M的位置,使得平面CA1C1和平面MA1C1所成的角(锐角)的余弦值是$\frac{{\sqrt{3}}}{3}$.
分析 (Ⅰ)由B1C1∥BC,可得B,B1,C1,C四点共面,延长CC1,BB1交于点D,连接A1D,由题意可证四边形AA1DB1为平行四边形.从而得到AB1∥A1D,然后由线面平行的判定得到AB1∥平面A1C1C;
(Ⅱ)由已知通过解三角形得到A1A⊥AC,AB⊥AC,然后建立如图所示的空间直角坐标系,设点M(0,t,0),(0≤t≤1),求出平面平面CA1C1的一个法向量$\overrightarrow{{n}_{1}}$,平面MA1C1的一个法向量$\overrightarrow{{n}_{2}}$,由题设平面CA1C1和平面MA1C1所成的角(锐角)的余弦值是$\frac{{\sqrt{3}}}{3}$列式求得t,则答案可求.
解答 (Ⅰ)证明:如图,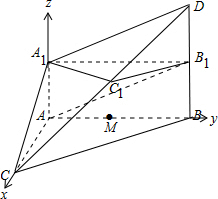 ∵B1C1∥BC,∴B,B1,C1,C四点共面,延长CC1,BB1交于点D,连接A1D,
∵B1C1∥BC,∴B,B1,C1,C四点共面,延长CC1,BB1交于点D,连接A1D,
∵BC=2B1C1,∴B1D=BB1,
又ABB1A1为正方形,∴B1D∥AA1,B1D=AA1,
∴四边形AA1DB1为平行四边形.
∴AB1∥A1D,又A1D?平面A1C1C,AB1?平面A1C1C,
∴AB1∥平面A1C1C;
(Ⅱ)解:∵四边形ABB1A1为正方形,
∴A1A=AB=AC=1,A1A⊥AB,
又△A1BC是等边三角形,∴${A}_{1}C=BC={A}_{1}B=\sqrt{2}$,
∴${A}_{1}{A}^{2}+A{C}^{2}={A}_{1}{C}^{2},A{C}^{2}+A{B}^{2}=B{C}^{2}$,
∴∠A1AC=90°,∠BAC=90°,即A1A⊥AC,AB⊥AC.
故建立如图所示的空间直角坐标系,
则C(1,0,0),A1(0,0,1),${C}_{1}(\frac{1}{2},\frac{1}{2},1)$,
设点M(0,t,0),(0≤t≤1),
则向量$\overrightarrow{C{A}_{1}}=(-1,0,1)$,
$\overrightarrow{{A}_{1}{C}_{1}}=(\frac{1}{2},\frac{1}{2},0),\overrightarrow{{A}_{1}M}=(0,t,-1)$,
设平面CA1C1的一个法向量为$\overrightarrow{{n}_{1}}=({x}_{1},{y}_{1},{z}_{1})$,
则由$\overrightarrow{{n}_{1}}•\overrightarrow{C{A}_{1}}=0,\overrightarrow{{n}_{1}}•\overrightarrow{{A}_{1}{C}_{1}}=0$.
得$\left\{\begin{array}{l}{-{x}_{1}+{z}_{1}=0}\\{\frac{1}{2}{x}_{1}+\frac{1}{2}{z}_{1}=0}\end{array}\right.$,令z1=1,则$\overrightarrow{{n}_{1}}=(1,-1,1)$.
设平面MA1C1的一个法向量为$\overrightarrow{{n}_{2}}=({x}_{2},{y}_{2},{z}_{2})$,
则由$\overrightarrow{{n}_{2}}•\overrightarrow{{A}_{1}{C}_{1}}=0,\overrightarrow{{n}_{2}}•\overrightarrow{AM}=0$,得
$\left\{\begin{array}{l}{\frac{1}{2}{x}_{2}+\frac{1}{2}{y}_{2}=0}\\{t{y}_{2}-{z}_{2}=0}\end{array}\right.$,令y2=1,得$\overrightarrow{{n}_{2}}=(-1,1,t)$,
∴由题设得$|cos<\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}>|=|\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}|=\frac{\sqrt{3}}{3}$.
即$\frac{|-2+t|}{\sqrt{3}•\sqrt{2+{t}^{2}}}=\frac{\sqrt{3}}{3}$,
又0≤t≤1,解得t=$\frac{1}{2}$.
即点M在线段AB的中点时,平面CA1C1和平面MA1C1所成角的余弦值为$\frac{\sqrt{3}}{3}$.
点评 本题考查了空间直线和平面的位置关系,考查了利用空间向量求二面角的平面角,是中档题.

 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是一个直角梯形,AB∥CD,∠ABC=90°,CD=3,BC=2,AB=A1B=5.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是一个直角梯形,AB∥CD,∠ABC=90°,CD=3,BC=2,AB=A1B=5. 如图,在正三棱柱ABC-A1B1C1中(底面为正三角形且侧棱垂直于底面的三棱柱叫正三棱柱),各棱长都是4,D是BC的中点.
如图,在正三棱柱ABC-A1B1C1中(底面为正三角形且侧棱垂直于底面的三棱柱叫正三棱柱),各棱长都是4,D是BC的中点. 如图,AB⊥平面BCD,AB=BC=CD=1,AD与平面BCD成45°的角,
如图,AB⊥平面BCD,AB=BC=CD=1,AD与平面BCD成45°的角,