题目内容
如图所示,已知正方形ABCD的边长为2,AC∩BD=O.将正方形ABCD沿对角BD折起,得到三棱锥A-BCD.(1)求证:平面AOC⊥平面BCD;
(2)若三棱锥A-BCD的体积为
 ,求AC的长.
,求AC的长.
【答案】分析:(1)直接根据可得由正方形的性质可得AO⊥BD以及BD⊥CO,根据线面垂直的判定定理,可得AO⊥平面BCD,进而得到结论.
(2)先根据三棱锥的体积求出棱锥的高,再分二面角为钝角和锐角两种情况分别求出AC的长即可.
解答: (本小题满分14分)
(本小题满分14分)
解:(1)证明:因为ABCD是正方形,
所以BD⊥AO,BD⊥CO.…(1分)
在折叠后的△ABD和△BCD中,
仍有BD⊥AO,BD⊥CO.…(2分)
因为AO∩CO=O,所以BD⊥平面AOC.…(3分)
因为BD?平面BCD,
所以平面AOC⊥平面BCD.…(4分)
(2)解:设三棱锥A-BCD的高为h,
由于三棱锥A-BCD的体积为 ,
,
所以 .…(5分)
.…(5分)
因为 ,所以
,所以 .…(6分)
.…(6分)
以下分两种情形求AC的长:
①当∠AOC为钝角时,如图,过点A作CO的垂线交CO的延长线于点H,
由(1)知BD⊥平面AOC,所以BD⊥AH.
又CO⊥AH,且CO∩BD=O,所以AH⊥平面BCD.
所以AH为三棱锥A-BCD的高,即 .…(7分)
.…(7分)
在Rt△AOH中,因为 ,
,
所以 =
= .…(8分)
.…(8分)
在Rt△ACH中,因为 ,
,
则 .…(9分)
.…(9分)
所以 .…(10分)
.…(10分)
②当∠AOC为锐角时,如图,过点A作CO的垂线交CO于点H,
由(1)知BD⊥平面AOC,所以BD⊥AH.
又CO⊥AH,且CO∩BD=O,所以AH⊥平面BCD.
所以AH为三棱锥A-BCD的高,即 .…(11分)
.…(11分)
 在Rt△AOH中,因为
在Rt△AOH中,因为 ,
,
所以 =
= .…(12分)
.…(12分)
在Rt△ACH中,因为 ,
,
则 .…(13分)
.…(13分)
所以 .
.
综上可知,AC的长为 或
或 .…(14分)
.…(14分)
点评:本题主要考察面面垂直的判定以及线段长度的计算.一般在证明面面垂直时,常转化为证线线垂直,得线面垂直,进而得到结论.
(2)先根据三棱锥的体积求出棱锥的高,再分二面角为钝角和锐角两种情况分别求出AC的长即可.
解答:
 (本小题满分14分)
(本小题满分14分)解:(1)证明:因为ABCD是正方形,
所以BD⊥AO,BD⊥CO.…(1分)
在折叠后的△ABD和△BCD中,
仍有BD⊥AO,BD⊥CO.…(2分)
因为AO∩CO=O,所以BD⊥平面AOC.…(3分)
因为BD?平面BCD,
所以平面AOC⊥平面BCD.…(4分)
(2)解:设三棱锥A-BCD的高为h,
由于三棱锥A-BCD的体积为
 ,
,所以
 .…(5分)
.…(5分)因为
 ,所以
,所以 .…(6分)
.…(6分)以下分两种情形求AC的长:
①当∠AOC为钝角时,如图,过点A作CO的垂线交CO的延长线于点H,
由(1)知BD⊥平面AOC,所以BD⊥AH.
又CO⊥AH,且CO∩BD=O,所以AH⊥平面BCD.
所以AH为三棱锥A-BCD的高,即
 .…(7分)
.…(7分)在Rt△AOH中,因为
 ,
,
所以
 =
= .…(8分)
.…(8分)在Rt△ACH中,因为
 ,
,则
 .…(9分)
.…(9分)所以
 .…(10分)
.…(10分)②当∠AOC为锐角时,如图,过点A作CO的垂线交CO于点H,
由(1)知BD⊥平面AOC,所以BD⊥AH.
又CO⊥AH,且CO∩BD=O,所以AH⊥平面BCD.
所以AH为三棱锥A-BCD的高,即
 .…(11分)
.…(11分) 在Rt△AOH中,因为
在Rt△AOH中,因为 ,
,所以
 =
= .…(12分)
.…(12分)在Rt△ACH中,因为
 ,
,则
 .…(13分)
.…(13分)所以
 .
.综上可知,AC的长为
 或
或 .…(14分)
.…(14分)点评:本题主要考察面面垂直的判定以及线段长度的计算.一般在证明面面垂直时,常转化为证线线垂直,得线面垂直,进而得到结论.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
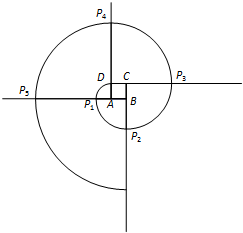 (2011•丰台区二模)如图所示,已知正方形ABCD的边长为1,以A为圆心,AD长为半径画弧,交BA的延长线于P1,然后以B为圆心,BP1长为半径画弧,交CB的延长线于P2,再以C为圆心,CP2长为半径画弧,交DC的延长线于P3,再以D为圆心,DP3长为半径画弧,交AD的延长线于P4,再以A为圆心,AP4长为半径画弧,…,如此继续下去,画出的第8道弧的半径是
(2011•丰台区二模)如图所示,已知正方形ABCD的边长为1,以A为圆心,AD长为半径画弧,交BA的延长线于P1,然后以B为圆心,BP1长为半径画弧,交CB的延长线于P2,再以C为圆心,CP2长为半径画弧,交DC的延长线于P3,再以D为圆心,DP3长为半径画弧,交AD的延长线于P4,再以A为圆心,AP4长为半径画弧,…,如此继续下去,画出的第8道弧的半径是
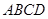 和矩形
和矩形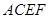 所在的平面互相垂直,
所在的平面互相垂直,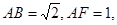
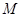 是线段
是线段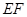 的中点。
的中点。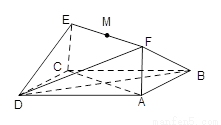
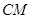 ∥平面
∥平面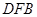
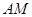 与
与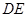 所成的角的余弦值。
所成的角的余弦值。