题目内容
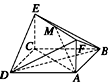
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=![]() ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
求证:
(1)AM∥平面BDE;
(2)AM⊥平面BDF.
证明略
解析:
(1)建立如图所示的空间直角坐标系,
设AC∩BD=N,连接NE.
则点N、E的坐标分别为![]() 、(0,0,1).
、(0,0,1).
 ∴
∴![]() =
=![]() .
.
又点A、M的坐标分别是
(![]() ,
,![]() ,0)、
,0)、![]() ,
,
∴![]() =
=![]() .
.
∴![]() =
=![]() 且NE与AM不共线.∴NE∥AM.
且NE与AM不共线.∴NE∥AM.
又∵NE![]() 平面BDE,AM
平面BDE,AM![]() 平面BDE,
平面BDE,
∴AM∥平面BDE.
(2)由(1)知![]() =
=![]() ,
,
∵D(![]() ,0,0),F(
,0,0),F(![]() ,
,![]() ,1),∴
,1),∴![]() =(0,
=(0,![]() ,1).
,1).
∴![]() ·
·![]() =0.∴
=0.∴![]() ⊥
⊥![]() .
.
同理![]() ⊥
⊥![]() .又DF∩BF=F,∴AM⊥平面BDF.
.又DF∩BF=F,∴AM⊥平面BDF.

练习册系列答案
相关题目
 如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
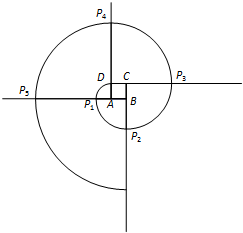 (2011•丰台区二模)如图所示,已知正方形ABCD的边长为1,以A为圆心,AD长为半径画弧,交BA的延长线于P1,然后以B为圆心,BP1长为半径画弧,交CB的延长线于P2,再以C为圆心,CP2长为半径画弧,交DC的延长线于P3,再以D为圆心,DP3长为半径画弧,交AD的延长线于P4,再以A为圆心,AP4长为半径画弧,…,如此继续下去,画出的第8道弧的半径是
(2011•丰台区二模)如图所示,已知正方形ABCD的边长为1,以A为圆心,AD长为半径画弧,交BA的延长线于P1,然后以B为圆心,BP1长为半径画弧,交CB的延长线于P2,再以C为圆心,CP2长为半径画弧,交DC的延长线于P3,再以D为圆心,DP3长为半径画弧,交AD的延长线于P4,再以A为圆心,AP4长为半径画弧,…,如此继续下去,画出的第8道弧的半径是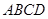 和矩形
和矩形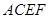 所在的平面互相垂直,
所在的平面互相垂直,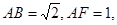
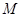 是线段
是线段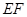 的中点。
的中点。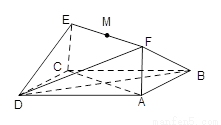
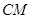 ∥平面
∥平面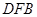
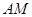 与
与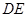 所成的角的余弦值。
所成的角的余弦值。