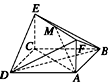
题目内容
如图所示,已知正方形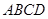 和矩形
和矩形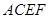 所在的平面互相垂直,
所在的平面互相垂直,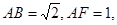
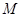 是线段
是线段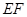 的中点。
的中点。
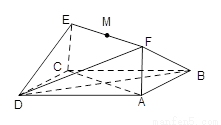
(1)证明: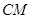 ∥平面
∥平面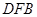
(2)求异面直线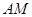 与
与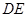 所成的角的余弦值。
所成的角的余弦值。
【答案】
(1)建立空间直角坐标系,用坐标表示点与向量,证明CM与平面BDF的法向量垂直,即可证得结论;
(2)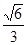
【解析】
试题分析:(1)证明:建立如图所示的空间直角坐标系,则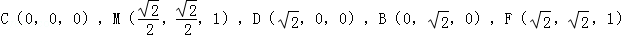 …(2分)
…(2分)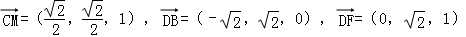
设平面DBF的一个法向量为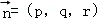 ,则
,则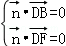 ,
,
∴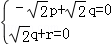
取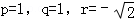 ,
,
得平面DBF的一个法向量为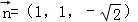 ,…(6分)
,…(6分)
因为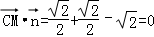 ,
,
所以 ,
,
又因为直线CM?平面DBF内,所以CM∥平面BDF.…(6分)
(2)结合上一问可知求异面直线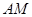 与
与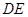 所成的角的余弦值,只要确定出向量AM和向量DE的坐标即可,结合平面向量的夹角公式来得到为
所成的角的余弦值,只要确定出向量AM和向量DE的坐标即可,结合平面向量的夹角公式来得到为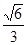
考点:线面平行,异面直线的角
点评:本题考查线面平行,考查面面角,解题的关键是建立空间直角坐标系,用坐标表示点与向量,利用向量的数量积求解

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
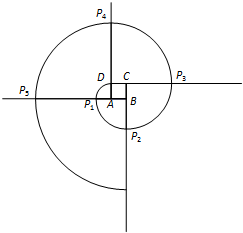 (2011•丰台区二模)如图所示,已知正方形ABCD的边长为1,以A为圆心,AD长为半径画弧,交BA的延长线于P1,然后以B为圆心,BP1长为半径画弧,交CB的延长线于P2,再以C为圆心,CP2长为半径画弧,交DC的延长线于P3,再以D为圆心,DP3长为半径画弧,交AD的延长线于P4,再以A为圆心,AP4长为半径画弧,…,如此继续下去,画出的第8道弧的半径是
(2011•丰台区二模)如图所示,已知正方形ABCD的边长为1,以A为圆心,AD长为半径画弧,交BA的延长线于P1,然后以B为圆心,BP1长为半径画弧,交CB的延长线于P2,再以C为圆心,CP2长为半径画弧,交DC的延长线于P3,再以D为圆心,DP3长为半径画弧,交AD的延长线于P4,再以A为圆心,AP4长为半径画弧,…,如此继续下去,画出的第8道弧的半径是