题目内容
若直线y=x+m与曲线x=
有且只有一个公共点,则实数m的取值范围是
| 2y-y2 |
0<m≤2,或m=1-
| 2 |
0<m≤2,或m=1-
.| 2 |
分析:曲线x=
代表以点(0,1)为圆心,1为半径的圆的右半圆,而直线y=x+m的斜率为1,截距为m,在同一个坐标系中作出它们的图象,数形结合可得.
| 2y-y2 |
解答:解:对x=
平方可得x2+y2-2y=0,整理可得x2+(y-1)2=1,
故曲线x=
代表以点(0,1)为圆心,1为半径的圆的右半圆,
而直线y=x+m的斜率为1,截距为m,在同一个坐标系中作出它们的图象:
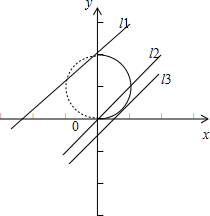
由图象可得当直线介于l1,l2之间,或为l3时两图象有且只有一个公共点,
由l3为相切可得
=1,解得m=1-
,或m=1+
,(舍去)
故当0<m≤2或m=1-
时,满足题意,
故答案为:0<m≤2,或m=1-
| 2y-y2 |
故曲线x=
| 2y-y2 |
而直线y=x+m的斜率为1,截距为m,在同一个坐标系中作出它们的图象:

由图象可得当直线介于l1,l2之间,或为l3时两图象有且只有一个公共点,
由l3为相切可得
| |0-1+m| | ||
|
| 2 |
| 2 |
故当0<m≤2或m=1-
| 2 |
故答案为:0<m≤2,或m=1-
| 2 |
点评:本题考查直线与圆相交的性质,数形结合是解决问题的关键,属中档题.

练习册系列答案
相关题目
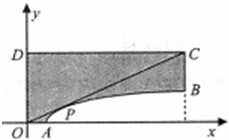 已知图形OAPBCD是由不等式组
已知图形OAPBCD是由不等式组