题目内容
已知焦点在x轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点A (0,![]() )为圆心,1为半径的圆相切,又知C的一个焦点与A关于y = x对称.
)为圆心,1为半径的圆相切,又知C的一个焦点与A关于y = x对称.
(1)求双曲线C的方程;
(2)若Q是双曲线线C上的任一点,F1,F2为双曲线C的左、右两个焦点,从F1引∠F1QF2的平分线的垂线,垂足为N,试求点N的轨迹方程;
(3)设直线y = mx + 1与双曲线C的左支交于A、B两点,另一直线l经过M (–2,0)及AB的中点,求直线l在y轴上的截距b的取值范围.
x2 – y2 = 1 ,x2 + y2 = 1 (x≠![]() ),(–∞,– 2 –
),(–∞,– 2 –![]() )∪(2,+∞)
)∪(2,+∞)
解析:
解:设双曲线C的渐近线为y = kx,即kx – y = 0.
∵渐近线与x2 + (y – ![]() )2 = 1相切,∴
)2 = 1相切,∴![]() ,∴双曲线C的渐近线为y = ±x,∴设双曲线方程为x2 – y2 = a2.∵A (0,
,∴双曲线C的渐近线为y = ±x,∴设双曲线方程为x2 – y2 = a2.∵A (0,![]() )关于y = x的对称点为(
)关于y = x的对称点为(![]() ,0),∴由题意知,双曲线的一个焦点为(
,0),∴由题意知,双曲线的一个焦点为(![]() ,0),
,0),
∴C = ![]() .∴2a2 = 2,a2 = 1,∴双曲线C的方程为x2 – y2 = 1.
.∴2a2 = 2,a2 = 1,∴双曲线C的方程为x2 – y2 = 1.
(2)若Q在双曲线的右支上,则延长QF2到T,使|QT| = |QF1|;若Q在双曲线的左支上,则在QF2上取一点T,使|QT| = |QF1|.根据双曲线的定义,|TF2| = 2.∴T在以F2 (![]() ,0)为圆心,2为半径的圆上,∴点T的轨迹方程是(x –
,0)为圆心,2为半径的圆上,∴点T的轨迹方程是(x –![]() )2 + y2 = 4 (x≠0) ①
)2 + y2 = 4 (x≠0) ①
易知,点N是线段F1T的中点.
设N (x,y),T (x0,y0),则 代入①得,N点的轨迹方程为
代入①得,N点的轨迹方程为
x2 + y2 = 1 (x≠![]() )
)
(3)由![]() 得 (1 – m2) x2 – 2mx – 2 = 0,依题意有
得 (1 – m2) x2 – 2mx – 2 = 0,依题意有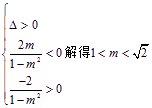
∵AB中点为![]() ,∴l的方程为y =
,∴l的方程为y = ![]() .
.
令x = 0得 b = 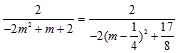
∵m∈(1,![]() ) ∴–2(m –
) ∴–2(m – ![]() )2 +
)2 + ![]() ∈(–2 +
∈(–2 + ![]() ,1)
,1)
∴b的范围是(–∞,– 2 –![]() )∪(2,+∞).
)∪(2,+∞).

 的焦点F与双曲
的焦点F与双曲 的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且
的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且 ,则A点的横坐标为
,则A点的横坐标为 B.3 C.
B.3 C. D.4
D.4