题目内容
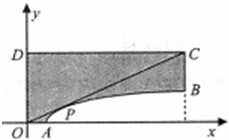 已知图形OAPBCD是由不等式组
已知图形OAPBCD是由不等式组
|
(1)证明:直线OC与曲线段相切;
(2)若过P点作曲线的切线交图形的边界于M,N,求图形被切线所截得的左上部分的面积的最小值.
分析:(1)设点O,C,P的坐标,利用导数的几何意义得到在点P处的切线的斜率,得到切线方程,根据切线方程过点O,可得切线方程,点C坐标满足切线方程,故点C在切线上,故可证得结论;
(2)根据(1)的结论,可得过点P的切线方程,根据点P横坐标的取值范围进行分类讨论,当1≤x0≤e时,切线交OA于点M,交CD于点N,可求得M,N的坐标,表示出图形被切线所截得的左上部分的面积S的表达式,利用导数即可求得最小值,当e≤x0≤e2时,切线交OD于点M,交BC于点N,可求得M,N的坐标,表示出图形被切线所截得的左上部分的面积S的表达式,利用导数即可求得最小值,最后比较两种情况中的最小值,即可确定答案.
(2)根据(1)的结论,可得过点P的切线方程,根据点P横坐标的取值范围进行分类讨论,当1≤x0≤e时,切线交OA于点M,交CD于点N,可求得M,N的坐标,表示出图形被切线所截得的左上部分的面积S的表达式,利用导数即可求得最小值,当e≤x0≤e2时,切线交OD于点M,交BC于点N,可求得M,N的坐标,表示出图形被切线所截得的左上部分的面积S的表达式,利用导数即可求得最小值,最后比较两种情况中的最小值,即可确定答案.
解答:解:(1)∵曲线段APB的方程为y=lnx(1≤x≤e2),P为曲线上的任一点,
又图形OAPBCD是由不等式组
围成的图形,
∴设O(0,0),C(e2,e),P(x0,lnx0),
∵y′=
,
∴过点P的切线的斜率k=
,
∴切线方程为:y-lnx0=
(x-x0),即y=
x+lnx0-1,①
若①式过点O,则由0=lnx0-1,解得x0=e,
∴切线方程为y=
,
又点C(e2,e)满足切线方程,
∴切线方程过点C,
∴直线OC与曲线相切
(2)由(1)可知,过点P的切线方程为y=
x+lnx0-1,
①当1≤x0≤e时,切线交OA于点M,交CD于点N,
∵y=
x+lnx0-1,
∴令y=0,解得x=x0(1-lnx0),
令y=e,解得x=x0(e+1-lnx0),
∴M(x0(1-lnx0),0),N(x0(e+1-lnx0),e),
∴图形被切线所截得的左上部分的面积S=
×e=ex0(
+1-lnx0),
∴S′=e(
-lnx0)>0,
∴S在[1,e]上单调递增,
∴当x0=1时,S取得最小值为e×1×(
+1-ln1)=
,
∴图形被切线所截得的左上部分的面积S的最小值为
;
②当e≤x0≤e2时,切线交OD于点M,交BC于点N,
∵y=
x+lnx0-1,
∴令x=0,解得y=lnx0-1,
令x=e2,解得y=
+lnx0-1,
∴M(0,lnx0-1),N(e2,
+lnx0-1),
∴图形被切线所截得的左上部分的面积S=
×e2=
(2e-2lnx0-
+2),
∴S′=
(
-
)=
(
),
令S′=0,解得x0=
,
当e≤x0≤
时,S′>0,当
<x0≤e2时,S′<0,
∴S在[e,
]上为单调递增函数,在(
,e2)上为单调递减函数,
∵当x0=e时,S=
×(2e-2-e+2)=
,
当x0=e2时,S=
×(2e-4-1+2)=
,
∵
>
,
∴S的最小值为
,
∴图形被切线所截得的左上部分的面积S的最小值为
.
综合①②,由于
>
,
∴当x0=1时,S的最小值为
,
故图形被切线所截得的左上部分的面积的最小值为
.
又图形OAPBCD是由不等式组
|
∴设O(0,0),C(e2,e),P(x0,lnx0),
∵y′=
| 1 |
| x |
∴过点P的切线的斜率k=
| 1 |
| x0 |
∴切线方程为:y-lnx0=
| 1 |
| x0 |
| 1 |
| x0 |
若①式过点O,则由0=lnx0-1,解得x0=e,
∴切线方程为y=
| x |
| e |
又点C(e2,e)满足切线方程,
∴切线方程过点C,
∴直线OC与曲线相切
(2)由(1)可知,过点P的切线方程为y=
| 1 |
| x0 |
①当1≤x0≤e时,切线交OA于点M,交CD于点N,
∵y=
| 1 |
| x0 |
∴令y=0,解得x=x0(1-lnx0),
令y=e,解得x=x0(e+1-lnx0),
∴M(x0(1-lnx0),0),N(x0(e+1-lnx0),e),
∴图形被切线所截得的左上部分的面积S=
| x0(1-lnx0)+x0(e+1-lnx0) |
| 2 |
| e |
| 2 |
∴S′=e(
| e |
| 2 |
∴S在[1,e]上单调递增,
∴当x0=1时,S取得最小值为e×1×(
| e |
| 2 |
| e(e+2) |
| 2 |
∴图形被切线所截得的左上部分的面积S的最小值为
| e(e+2) |
| 2 |
②当e≤x0≤e2时,切线交OD于点M,交BC于点N,
∵y=
| 1 |
| x0 |
∴令x=0,解得y=lnx0-1,
令x=e2,解得y=
| e2 |
| x0 |
∴M(0,lnx0-1),N(e2,
| e2 |
| x0 |
∴图形被切线所截得的左上部分的面积S=
e-(lnx0-1)+e-(
| ||
| 2 |
| e2 |
| 2 |
| e2 |
| x0 |
∴S′=
| e2 |
| 2 |
| e2 |
| x0 |
| 2 |
| x0 |
| e2 |
| 2 |
| e2-2x0 |
| x02 |
令S′=0,解得x0=
| e2 |
| 2 |
当e≤x0≤
| e2 |
| 2 |
| e2 |
| 2 |
∴S在[e,
| e2 |
| 2 |
| e2 |
| 2 |
∵当x0=e时,S=
| e2 |
| 2 |
| e3 |
| 2 |
当x0=e2时,S=
| e2 |
| 2 |
| e2(2e-3) |
| 2 |
∵
| e3 |
| 2 |
| e2(2e-3) |
| 2 |
∴S的最小值为
| e2(2e-3) |
| 2 |
∴图形被切线所截得的左上部分的面积S的最小值为
| e2(2e-3) |
| 2 |
综合①②,由于
| e2(2e-3) |
| 2 |
| e(e+2) |
| 2 |
∴当x0=1时,S的最小值为
| e(e+2) |
| 2 |
故图形被切线所截得的左上部分的面积的最小值为
| e(e+2) |
| 2 |
点评:本题考查了利用导数研究曲线上某点处的切线方程,利用导数研究函数的最值问题.导数的几何意义即在某点处的导数即该点处切线的斜率,解题时要注意运用切点在曲线上和切点在切线上.利用导数研究函数在闭区间上的最值,一般是求出导函数对应方程的根,然后求出跟对应的函数值,区间端点的函数值,然后比较大小即可得到函数在闭区间上的最值.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目