题目内容
如果ab=-1,那么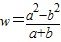 的取值范围是( )
的取值范围是( )A.(-∞,-2)∪(2,+∞)
B.(-∞,-2]∪[2,+∞)
C.(-2,2)
D.[-2,2]
【答案】分析:先将b用a表示,然后根据条件求出a的范围,讨论a的正负,利用基本不等式求出w的取值范围即可.
解答:解:∵ab=-1∴b=-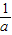
∴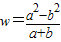 =a-b=a+
=a-b=a+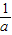
要使上式有意义a≠±1
当a>0时,a+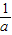 ≥2
≥2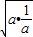 =2,等号取不到;
=2,等号取不到;
当a<0时,a+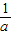 =-(-a-
=-(-a-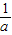 )≤-2
)≤-2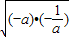 =-2,等号取不到;
=-2,等号取不到;
综上所述w的范围是(-∞,-2)∪(2,+∞)
故选A.
点评:本题主要考查了函数的值域,以及利用基本不等式求函数的值域,解题的关键注意a的范围,属于中档题.
解答:解:∵ab=-1∴b=-
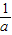
∴
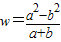 =a-b=a+
=a-b=a+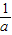
要使上式有意义a≠±1
当a>0时,a+
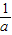 ≥2
≥2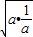 =2,等号取不到;
=2,等号取不到;当a<0时,a+
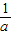 =-(-a-
=-(-a-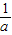 )≤-2
)≤-2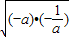 =-2,等号取不到;
=-2,等号取不到;综上所述w的范围是(-∞,-2)∪(2,+∞)
故选A.
点评:本题主要考查了函数的值域,以及利用基本不等式求函数的值域,解题的关键注意a的范围,属于中档题.

练习册系列答案
相关题目
直线l过点(-4,0)且与圆(x+1)2+(y-2)2=25交于A、B两点,如果|AB|=8,那么直线l的方程为( )
| A、5x+12y+20=0 | B、5x-12y+20=0或x+4=0 | C、5x-12y+20=0 | D、5x+12y+20=0或x+4=0 |
如果ab=-1,那么w=
的取值范围是( )
| a2-b2 |
| a+b |
| A、(-∞,-2)∪(2,+∞) |
| B、(-∞,-2]∪[2,+∞) |
| C、(-2,2) |
| D、[-2,2] |
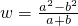 的取值范围是
的取值范围是